题目内容
函数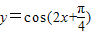 的图象的一条对称轴方程为( )
的图象的一条对称轴方程为( )A.
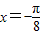
B.
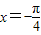
C.
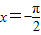
D.x=-π
【答案】分析:利用余弦函数的对称轴是过图象的最高点或最低点且且垂直于x轴的直线,由2x+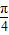 =kπ,k∈z,解出x=
=kπ,k∈z,解出x=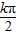 -
-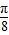 ,k∈z,分析各个选项是否满足此式可得答案.
,k∈z,分析各个选项是否满足此式可得答案.
解答:解:∵函数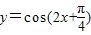 的图象的对称轴是过图象的顶点且垂直于x轴的直线,
的图象的对称轴是过图象的顶点且垂直于x轴的直线,
对称轴方程为2x+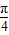 =kπ,即x=
=kπ,即x=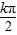 -
- ,k∈z,
,k∈z,
故选A.
点评:本题考查余弦函数的对称性,判断对称轴方程为 2x+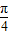 =kπ,k∈z是解题的关键.
=kπ,k∈z是解题的关键.
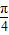 =kπ,k∈z,解出x=
=kπ,k∈z,解出x=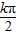 -
-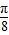 ,k∈z,分析各个选项是否满足此式可得答案.
,k∈z,分析各个选项是否满足此式可得答案.解答:解:∵函数
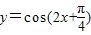 的图象的对称轴是过图象的顶点且垂直于x轴的直线,
的图象的对称轴是过图象的顶点且垂直于x轴的直线,对称轴方程为2x+
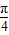 =kπ,即x=
=kπ,即x=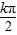 -
- ,k∈z,
,k∈z,故选A.
点评:本题考查余弦函数的对称性,判断对称轴方程为 2x+
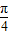 =kπ,k∈z是解题的关键.
=kπ,k∈z是解题的关键. 
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
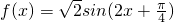 ,给出下列四个命题:
,给出下列四个命题: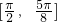 上是减函数;
上是减函数; 是函数f(x)的图象的一条对称;
是函数f(x)的图象的一条对称;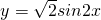 的图象向左平移
的图象向左平移 而得到.
而得到.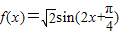 ,给出下列三个命题:
,给出下列三个命题: 上是减函数;
上是减函数; 是函数f(x)的图象的一条对称;
是函数f(x)的图象的一条对称; 的图象向左平移
的图象向左平移 而得到.
而得到.