题目内容
设∠POQ=60°,在OP、OQ上分别有动点A、B,若
•
=6,△AOB的重心是G,则|
|的最小值是
| OA |
| OB |
| OG |
2
2
.分析:根据△AOB的重心是G,可得
=
×
×(
+
)=
,再结合基本不等式,即可求得结论.
| OG |
| 2 |
| 3 |
| 1 |
| 2 |
| OA |
| OB |
| ||||
| 3 |
解答:解:∵△AOB的重心是G,∴
=
×
×(
+
)=
设|
|=m,|
|=n,则
∵
•
=6,∠POQ=60°,
∴mn=12
∴|
|2=(
)2=
(m2+n2+12)≥
(2mn+12)=4
当且仅当m=n=2
时,则|
|的最小值是2
故答案为:2
| OG |
| 2 |
| 3 |
| 1 |
| 2 |
| OA |
| OB |
| ||||
| 3 |
设|
| OA |
| OB |
∵
| OA |
| OB |
∴mn=12
∴|
| OG |
| ||||
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
当且仅当m=n=2
| 3 |
| OG |
故答案为:2
点评:本题考查向量知识的运用,考查基本不等式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 ·
· =6, △OAB的重心是G,则|
=6, △OAB的重心是G,则| |
的最小值是( )
|
的最小值是( ) ·
· =6,
△OAB的重心是G,则|
=6,
△OAB的重心是G,则| |
的最小值是( )
|
的最小值是( )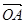 ·
· =6, △OAB的重心是G,则|
=6, △OAB的重心是G,则| |
的最小值是( )
|
的最小值是( )