题目内容
设直线l的方程为x+ycosθ+3=0(θ∈R),则直线l的倾斜角α的取值范围( )
分析:根据题意,分cosθ=0和cosθ≠0两种情况加以讨论,结合余弦函数的值域和正切函数的单调性,即可得到直线l的倾斜角α的取值范围.
解答:解:由题意,当cosθ=0时,l的方程化x+3=0,
此时,直线l的倾斜角α为90°;
当cosθ≠0时,将直线化成斜截式:y=-
x-
直线x+ycosθ+3=0(θ∈R)的倾斜角为α,可得tanα=-
∵-1≤cosθ≤1且cosθ≠0
∴tanα=-
∈(-∞,-1]∪[1,+∞),
∵0°≤α<180°,∴结合正切函数的单调性,可得45°≤α≤135°,且α≠90°
综上所述,直线l的倾斜角α的取值范围是:[
,
]
故选:C
此时,直线l的倾斜角α为90°;
当cosθ≠0时,将直线化成斜截式:y=-
| 1 |
| cosθ |
| 3 |
| cosθ |
直线x+ycosθ+3=0(θ∈R)的倾斜角为α,可得tanα=-
| 1 |
| cosθ |
∵-1≤cosθ≤1且cosθ≠0
∴tanα=-
| 1 |
| cosθ |
∵0°≤α<180°,∴结合正切函数的单调性,可得45°≤α≤135°,且α≠90°
综上所述,直线l的倾斜角α的取值范围是:[
| π |
| 4 |
| 3π |
| 4 |
故选:C
点评:本题给出直线方程含有余弦函数系数的形式,求直线倾斜角范围,着重考查了余弦函数的值域和正切函数的单调性等知识,属于基础题.

练习册系列答案
相关题目
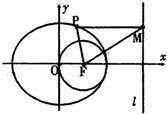 如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4
如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4