题目内容
如图,在△ABC中,∠C=90°,sinB= ,F是AB上一点,过点F作DF⊥AB于F,交BC城E,交AC延长线于D,连CF,若S△BEF=4S△CDE,CE=5,
,F是AB上一点,过点F作DF⊥AB于F,交BC城E,交AC延长线于D,连CF,若S△BEF=4S△CDE,CE=5,(1)求AC的长 (2)求S△CEF.

【答案】分析:(1)易得△BFE∽△DCE,根据面积之间的关系式可得到相应的相似比,利用CE长,那么可求得BE长,进而求得BC,利用sinB的值和勾股定理即可求得AC长;
(2)利用sinB可求得BF、FE,由于△CEF和△BEF同高,那么面积的比就等于底边的比.按此计算即可.
解答:解:(1)∵∠BFE=∠BCD=90°,∠FEB=∠DEC
∴△BFE∽△DCF
∵S△BEF=4S△CDE,
∴S△BEF:S△DEC=4:1
∴EF:EC=2:1
∵CE=5,∴EF=10,
∵sinB= ,∴BE=
,∴BE=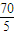 ,∴BC=
,∴BC=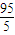
设AC=5k,则AB=7k
∵AB2-AC2=BC2,
∴49k2-25k2=( )2
)2
解得k=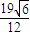 (负值舍去)
(负值舍去)
∴AC=5×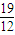
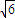 =
=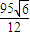 ;
;
(2)∵sinB= ,BE=
,BE=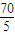 ,EF=10;
,EF=10;
∴BF=4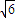
S△BFE=BF×EF÷2=20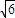
∵BE:EC=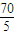 :5
:5
∴S△CEF=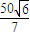 .
.
点评:本题以三角形为载体,主要考查了相似三角形的性质以及解直角三角形的应用等知识.
(2)利用sinB可求得BF、FE,由于△CEF和△BEF同高,那么面积的比就等于底边的比.按此计算即可.
解答:解:(1)∵∠BFE=∠BCD=90°,∠FEB=∠DEC
∴△BFE∽△DCF
∵S△BEF=4S△CDE,
∴S△BEF:S△DEC=4:1
∴EF:EC=2:1
∵CE=5,∴EF=10,
∵sinB=
 ,∴BE=
,∴BE=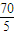 ,∴BC=
,∴BC=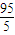
设AC=5k,则AB=7k
∵AB2-AC2=BC2,
∴49k2-25k2=(
 )2
)2解得k=
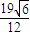 (负值舍去)
(负值舍去)∴AC=5×
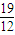
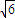 =
=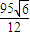 ;
;(2)∵sinB=
 ,BE=
,BE=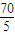 ,EF=10;
,EF=10;∴BF=4
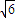
S△BFE=BF×EF÷2=20
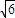
∵BE:EC=
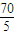 :5
:5∴S△CEF=
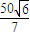 .
.点评:本题以三角形为载体,主要考查了相似三角形的性质以及解直角三角形的应用等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知