题目内容
 如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点B(0,-2
如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点B(0,-2| 2 |
(1)求BC边所在直线方程;
(2)圆M是△ABC的外接圆,求圆M的方程;
(3)若DE是圆M的任一条直径,试探究
| PD |
| PE |
分析:(1)用斜率公式求出 AB的斜率 KAB,根据垂直关系可得BC的斜率 KBC,用点斜式求得BC边所在直线方程.
(2)在BC边所在直线方程中,令y=0,可得点 C的坐标,设△ABC的外接圆方程为 x2+y2+Dx+Ey+F=0,把 A、B、C三点的坐标分别代入,求出 D、E、F的值,即得△ABC的外接圆方程.
(3)由题意可得P(-1,0 ),△ABC的外接圆标准方程为 (x-1)2+y2=9,设
与
的夹角为θ,则
与
的夹角为π-θ,根据
•
=(
+
)•(
+
),求得结果.
(2)在BC边所在直线方程中,令y=0,可得点 C的坐标,设△ABC的外接圆方程为 x2+y2+Dx+Ey+F=0,把 A、B、C三点的坐标分别代入,求出 D、E、F的值,即得△ABC的外接圆方程.
(3)由题意可得P(-1,0 ),△ABC的外接圆标准方程为 (x-1)2+y2=9,设
| PS |
| SE |
| PS |
| SD |
| PD |
| PE |
| PS |
| SD |
| PS |
| SE |
解答:解:(1)AB的斜率 KAB=
=-
,∴KBC=
=
,
故求BC边所在直线方程为 y+2
=
(x-0),即 y=
x-2
.
(2)在BC边所在直线方程中,令y=0,可得 x=4,故 C(4,0).
设△ABC的外接圆方程为 x2+y2+Dx+Ey+F=0,把 A、B、C三点的坐标分别代入可得
,解得
,∴△ABC的外接圆方程为 x2+y2-2x-8=0.
(3)由题意可得P(-1,0 ),△ABC的外接圆标准方程为 (x-1)2+y2=9,
表示以S(1,0)为圆心,以3为半径的圆.
由于DE是圆M的任一条直径,设
与
的夹角为θ,则
与
的夹角为π-θ,
∴
•
=(
+
)•(
+
)=
2+
•
+
•
+
•
=4+|
|•|
|cosθ+|
|•|
|cos(π-θ)+(-SD2)=4+2×3cosθ-2×3cosθ-9=-5,
故
•
是定值,为-5.
-2
| ||
| 0+2 |
| 2 |
| -1 |
| KAB |
| ||
| 2 |
故求BC边所在直线方程为 y+2
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
(2)在BC边所在直线方程中,令y=0,可得 x=4,故 C(4,0).
设△ABC的外接圆方程为 x2+y2+Dx+Ey+F=0,把 A、B、C三点的坐标分别代入可得
|
|
(3)由题意可得P(-1,0 ),△ABC的外接圆标准方程为 (x-1)2+y2=9,
表示以S(1,0)为圆心,以3为半径的圆.
由于DE是圆M的任一条直径,设
| PS |
| SE |
| PS |
| SD |
∴
| PD |
| PE |
| PS |
| SD |
| PS |
| SE |
| PS |
| PS |
| SE |
| PS |
| SD |
| SD |
| SE |
=4+|
| PS |
| SE |
| PS |
| SD |
故
| PD |
| PE |
点评:本题考查用点斜式求直线方程,求圆的一般方程和标准方程,两个向量的数量积的定义,得到
•
=(
+
)•(
+
),是解题的关键.
| PD |
| PE |
| PS |
| SD |
| PS |
| SE |

练习册系列答案
相关题目
 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=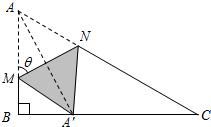 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC= (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答) (2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)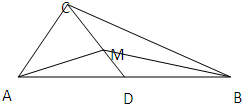 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.