题目内容
(本小题满分14分)函数f(x)=1-2a-2acosx-2sin2x的最小值为g(a)(a∈R).
(1)求g(a);
(2)若g(a)=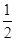 ,求a及此时f(x)的最大值.
,求a及此时f(x)的最大值.
【答案】
(1)见解析; (2) a=-1. 此时f(x)取得最大值为5.
【解析】(1)f(x)=1-2a-2acosx-2sin2x=2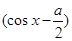 2-
2-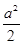 -2a-1.-1≤cosx≤1.转化为二次函数问题解决.
-2a-1.-1≤cosx≤1.转化为二次函数问题解决.
(2)在第(1)问的基础上,根据g(a)=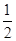 ,建立关于a的方程求解即可.
,建立关于a的方程求解即可.
解:(1)由f(x)=1-2a-2acosx-2sin2x
=1-2a-2acosx-2(1-cos2x)
=2cos2x-2acosx-(2a+1)
=2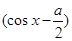 2-
2-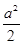 -2a-1.这里-1≤cosx≤1. …………4分
-2a-1.这里-1≤cosx≤1. …………4分
①若-1≤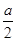 ≤1,即-2≤a≤2,则当cosx=
≤1,即-2≤a≤2,则当cosx=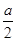 时,f(x)min=-
时,f(x)min=-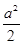 -2a-1;…………5分
-2a-1;…………5分
②若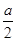 >1,则当cosx=1时,f(x)min=1-4a;…………6分
>1,则当cosx=1时,f(x)min=1-4a;…………6分
③若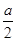 <-1,则当cosx=-1时,f(x)min=1. …………7分
<-1,则当cosx=-1时,f(x)min=1. …………7分
因此g(a)=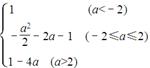 .…………8分
.…………8分
(2)∵g(a)=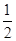 .
.
∴①若a>2,则有1-4a=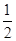 ,得a=
,得a=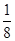 ,矛盾; …………10分
,矛盾; …………10分
②若-2≤a≤2,则有-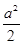 -2a-1=
-2a-1=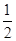 ,
,
即a2+4a+3=0,∴a=-1或a=-3(舍). …………12分
∴g(a)=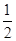 时,a=-1. 此时f(x)=2
时,a=-1. 此时f(x)=2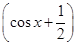 2+
2+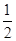 ,
,
当cosx=1时,f(x)取得最大值为5. …………14分

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)