题目内容
(本小题15分)在各项为正的数列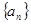 中,数列的前n项和
中,数列的前n项和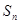 满足
满足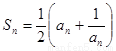
(1) 求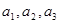 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列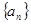 的通项公式并证明,(3) 求
的通项公式并证明,(3) 求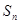
解:
(1)a1=1,a2=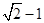 ,a3=
,a3=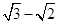 ;
;
(2)数列{an}的通项公式可能是:an=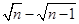 ,证明见解析。
,证明见解析。
(3)Sn=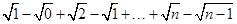 =
=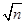
【解析】本试题主要是考查了数列的通项公式与前n项和的关系式的运用,令值的思想得到前几项,然后归纳猜想数列的通项公式,并运用数学归纳法证明,
(1)由题意可知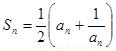 ,那么对于n令值,那么可知a2=
,那么对于n令值,那么可知a2=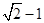
a3=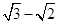
(2)根据上一问的结论,数列{an}的通项公式可能是:an=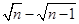 ,然后运用数学归纳法分两步骤证明即可。
,然后运用数学归纳法分两步骤证明即可。
(3)因为通项公式累加可以得到前n项和的结论。
解:
(1)S1=1/2(a1+1/a1)
又S1=a1
故1/2(a1+1/a1)=a1
即a12=1 因为a1>0
故a1=1
S2=1/2(a2+1/a2)
又S2=a1+a2=1+a2
故1/2(a2+1/a2)=1+a2 (a2>0)
解得:a2=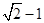
同理:a3=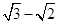
(2)从(1)中可看出:数列{an}的通项公式可能是:an=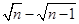
假设an=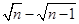 成立
成立
证明:
① 当n=1时,an=1=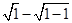 假设成立
假设成立
② 当n=2时,an=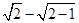 =
=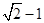 假设成立
假设成立
③ 假设n=i时,假设成立,即
ai=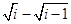
Si=(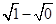 +(
+(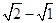 )+(
)+(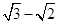 )+…+(
)+…+(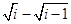 )=
)=
那么,当n=i+1时
由sn=1/2(an+1/an)得
Si+1=1/2(ai+1+1/ai+1)
ai+1=Si+1-Si=1/2(ai+1+1/ai+1)- 
解得:ai+1=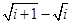 由①②③可证明假设an=
由①②③可证明假设an=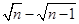 成立
成立
an通项公式为:an=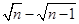
(3)Sn=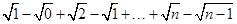 =
=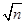

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案(本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
| 第一车间 | 第二车间 | 第三车间 | |
| 女工 | 173 | 100 |
|
| 男工 | 177 |
|
|
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知![]() ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.
.(本小题满分12分)某农场在相同条件下种植甲、乙两种水稻各100 亩,它们的收获情况如下:
甲 乙
| 亩产量(单位:千克) | 300 | 320 | 330 | 340 |
| 亩数 | 20 | 25 | 40 | 15 |
| 亩产量(单位:千克) | 310 | 320 | 330 | 340 |
| 亩数 | 30 | 20 | 40 | 10 |
试说明哪种水稻的产量比较稳定?
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,则样本中男、女生各有多少人;
(2)随机抽取8位同学,数学分数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定80分(含80分)以上为良好,90分(含90分)以上为优秀,在良好的条件下,求两科均为优秀的概率;
②若这8位同学的数学、物理分数事实上对应下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95[来源:Z&xx&k.Com] |
| 物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
根据上表数据可知,变量![]() 与
与![]() 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出![]() 与
与![]() 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式:![]() ,其中
,其中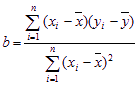 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
|
|
第一车间 |
第二车间 |
第三车间 |
|
女工 |
173 |
100 |
|
|
男工 |
177 |
|
|
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.