当a≠0时.函数y=ax+b和y=bax的图象只可能是( )A．B．C．D．题目和参考答案——青夏教育精英家教网——

题目内容

当a≠0时，函数y=ax+b和y=b^ax的图象只可能是（　　）

A．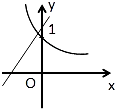

B．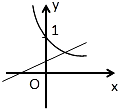

C．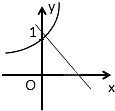

D．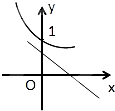

由一次函数的图象和性质可得：
A中，b＞1，a＞0，则b^a＞1，y=b^ax=（b^a）^x为单调增函数，故A不正确；
B中，0＜b＜1，a＞0，则0＜b^a＜1，y=b^ax=（b^a）^x为单调减函数，故B正确；
C中，b＞1，a＜0，则0＜b^a＜1，y=b^ax=（b^a）^x为单调减函数，C不对；
D中，0＜b＜1，a＜0，则b^a＞1，y=b^ax=（b^a）^x为单调增函数，D不对
故选B．

练习册系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

赢在起跑线天天100分小学优化测试卷系列答案

目标测试系列答案

单元评价卷宁波出版社系列答案

熠光传媒名师好卷系列答案

英才小灵通系列答案

顶尖训练系列答案

相关题目

已知函数?(x)=

，a为正常数．
（1）若f（x）=lnx+φ（x），且a=

，求函数f（x）的单调增区间；
（2）在（1）中当a=0时，函数y=f（x）的图象上任意不同的两点A（x₁，y₁），B（x₂，y₂），线段AB的中点为C（x₀，y₀），记直线AB的斜率为k，试证明：k＞f'（x₀）．
（3）若g（x）=|lnx|+φ（x），且对任意的x₁，x₂∈（0，2]，x₁≠x₂，都有

＜-1，求a的取值范围．

当a≠0时，函数y=ax+b和y=b^ax的图象只可能是（　　）

当a≠0时，函数y=ax+b和y=b^ax在同一坐标系内的大致图象是（　　）

下列命题中正确的是（　　）

A．当a=0时，函数y=x^a的图象是一条直线

B．幂函数的图象都经过（0，0），（1，1）两点

C．幂函数的y=x^a图象不可能在第四象限内

D．若幂函数y=x^a为奇函数，则在定义域内是增函数

（2013•莱芜二模）已知函数f（x）=ax+lnx，g（x）=e^x．
（I）当a≤0时，求f（x）的单调区间；
（Ⅱ）若不等式g(x)＜

有解，求实数m的取值菹围；
（Ⅲ）定义：对于函数y=F（x）和y=G（x）在其公共定义域内的任意实数x₀，称|F（x₀）-G（x₀）|的值为两函数在x₀处的差值．证明：当a=0时，函数y=f（x）和y=g（x）在其公共定义域内的所有差值都大干2．