题目内容
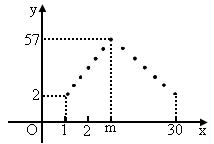
在4月份(共30天),有一新款服装投放某专卖店销售,日销售量(单位为件)f(x)关于时间n(1≤v≤30,n∈N*)的函数关系如图所示,其中函数f(n)的图象中的点位于斜率为5和-3的两条直线上,两直线的交点的横坐标为m,且第m天日销售量最大.(1)求f(n)的表达式,及前m天的销售总数;
(2)按规律,当该专卖店销售总数超过400件时,社会上流行该服装,而日销售量连续下降并低于30件时,该服装的流行会消失,试问该服装在社会上流行的天数是否会超过10天?并说明理由.
答案:
解析:
解析:
| (1)由图形知,当1≤n≤m且n∈N*时,f(n)=5n-3.
由f(m)=57得m=12.
前12天的销售总量为 5(1+2+3+…+12)-3×12=354件. (2)第13天的销售量为f(13)= -3×13+93=54件. 而354+54>400件, ∴从第14天开始销售总量超过400件,即开始流行. 设第n天的日销售量开始低于30件(12<n≤30),即f(n)=-3n+93<30,解得n>21. ∴从第22天开始日销售量低于30件, 即流行时间为14号至21号. ∴该服装流行时间不超过10天. |

练习册系列答案
相关题目
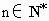 )的关系如图所示,其中函数f(n)图象中的点位于斜率为5和-3的两条直线上,两直线的交点的横坐标为m,且第m天日销售量最大.
)的关系如图所示,其中函数f(n)图象中的点位于斜率为5和-3的两条直线上,两直线的交点的横坐标为m,且第m天日销售量最大.