题目内容
（2012•张掖模拟）已知△OAB是以OB为斜边的等腰直角三角形，若OB=
，
=
+(1-λ)
且λ2＞1，则
•
的取值范围是（ ）
| 2 |
| OC |
| OA |
| OB |
| OC |
| AB |
分析：分别以AO，AB所在的直线为x轴，y轴建立直角坐标系，则可得
•
=1-λ，结合已知λ2＞1，可求
| OC |
| AB |
解答：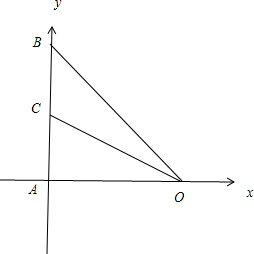
解：分别以AO，AB所在的直线为x轴，y轴建立直角坐标系，如图所示
由△OAB是以OB为斜边的等腰直角三角形，且OB=
可得AO=AB=1
则O（1，0），B（0，1），
=(0，1)
∵
=
+(1-λ)
=（-1，0）+（λ-1，1-λ）=（λ-2，1-λ）
∴
•
=1-λ
∵λ2＞1，即λ＞1或λ＜-1
∴1-λ＞2或1-λ＜0
故选A
解：分别以AO，AB所在的直线为x轴，y轴建立直角坐标系，如图所示由△OAB是以OB为斜边的等腰直角三角形，且OB=
| 2 |
则O（1，0），B（0，1），
| AB |
∵
| OC |
| OA |
| OB |
∴
| OC |
| AB |
∵λ2＞1，即λ＞1或λ＜-1
∴1-λ＞2或1-λ＜0
故选A
点评：本题主要考查了向量的数量积的坐标表示的应用，属于基础试题
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目