题目内容
已知二次函数f(x)=ax2+bx+c(a≠0)的导函数为f′(x),且f(-x)=f(x),f(1)=1,f′(-1)=-2.数列{an}满足a1=1,且当n≥2,n∈N*时,an=n2[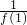 +
+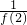 +…+
+…+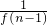 ].
].
(1)求函数f(x)的解析式;
(2)当n≥2且n∈N*时,比较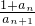 与
与 的大小.
的大小.
(3)比较(1+ )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )与4的大小.
)与4的大小.
解:(1)∵f(x)=ax2+bx+c,∴由f(-x)=f(x),有b=0,得f(x)=ax2+c.又f(1)=1,f′(-1)=-2,∴a+c=1,2a×(-1)=-2,∴a=1,c=0,∴f(x)=x2.
(2)∵f(n)=n2,∴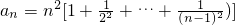 .,∴
.,∴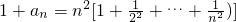 ,
,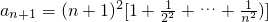 ,∴
,∴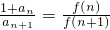 .
.
(3)由题意可得a2=4;当n=1时,有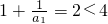 .当n≥2且n∈N*时,
.当n≥2且n∈N*时,
(1+ )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )=
)=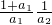
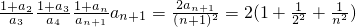
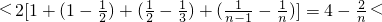 4(
4(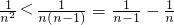 )
)
所以,对任意n∈N*有(1+ )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )<4.
)<4.
分析:(1)利用由f(-x)=f(x),有b=0,从而f(x)=ax2+c,f(1)=1,f′(-1)=-2,可求a、c的值,从而可求函数表达式;
(2)分别表示出分子、分母,进而可得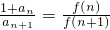 ;
;
(3)将连乘积表示为(1+ )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )=
)=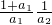
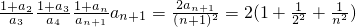 ,再用裂项求和法,利用
,再用裂项求和法,利用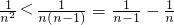 可得结论.
可得结论.
点评:本题考查数列与不等式的结合,考查裂项求和、放缩法,有一定的技巧.
(2)∵f(n)=n2,∴
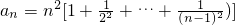 .,∴
.,∴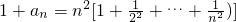 ,
,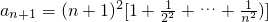 ,∴
,∴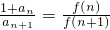 .
.(3)由题意可得a2=4;当n=1时,有
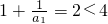 .当n≥2且n∈N*时,
.当n≥2且n∈N*时,(1+
 )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )=
)=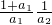
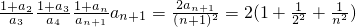
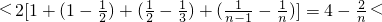 4(
4(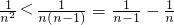 )
)所以,对任意n∈N*有(1+
 )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )<4.
)<4.分析:(1)利用由f(-x)=f(x),有b=0,从而f(x)=ax2+c,f(1)=1,f′(-1)=-2,可求a、c的值,从而可求函数表达式;
(2)分别表示出分子、分母,进而可得
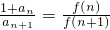 ;
;(3)将连乘积表示为(1+
 )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )=
)=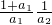
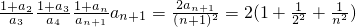 ,再用裂项求和法,利用
,再用裂项求和法,利用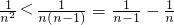 可得结论.
可得结论.点评:本题考查数列与不等式的结合,考查裂项求和、放缩法,有一定的技巧.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目