题目内容
已知f(3x)=4xlog23+233,则f(2)+f(4)+f(8)+…+f(28)的值是 .
2008
令3x=t,则x=log3t,
∴f(t)=4log23·log3t+233=4log2t+233,
∴f(2)+f(4)+f(8)+…+f(28)
=4(log22+log24+log28+…+log228)+8×233
=4·log2(2·22·23·…·28)+8×233=4·log2236+1864=4×36+1864=2008.
∴f(t)=4log23·log3t+233=4log2t+233,
∴f(2)+f(4)+f(8)+…+f(28)
=4(log22+log24+log28+…+log228)+8×233
=4·log2(2·22·23·…·28)+8×233=4·log2236+1864=4×36+1864=2008.

练习册系列答案
相关题目
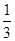 ×
×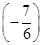 0+80.25×
0+80.25×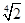 +(
+(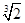 ×
×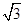 )6-
)6-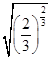 ;
;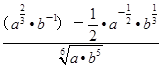 ;
;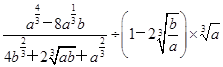
 )x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1-|x|),则关于h(x)有下列命题:
)x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1-|x|),则关于h(x)有下列命题: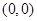 点
点 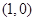 点
点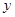 轴右侧
轴右侧 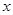 轴上方
轴上方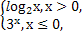 关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是( )
关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是( )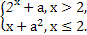 若f(x)的值域为R,则常数a的取值范围是( )
若f(x)的值域为R,则常数a的取值范围是( )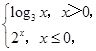 则f
则f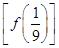 = ( ).
= ( ).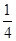
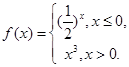 若
若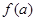 >1,则a的取值范围是
>1,则a的取值范围是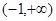
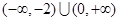
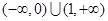
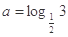 ,
,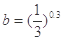 ,
,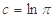 ,则( )
,则( )