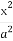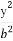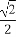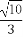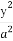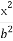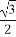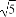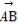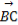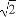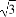ЬтФПФкШн
вбжЊдВCгыСНдВx2+(y+4)2=1,x2+(y-2)2=1ЭтЧа,дВCЕФдВаФЙьМЃЗНГЬЮЊL,ЩшLЩЯЕФЕугыЕуM(x,y)ЕФОрРыЕФзюаЁжЕЮЊm,ЕуF(0,1)гыЕуM(x,y)ЕФОрРыЮЊn.
(1)ЧѓдВCЕФдВаФЙьМЃLЕФЗНГЬ.
(2)ЧѓТњзуЬѕМўm=nЕФЕуMЕФЙьМЃQЕФЗНГЬ.
(3)дк(2)ЕФЬѕМўЯТ,ЪдЬНОПЙьМЃQЩЯЪЧЗёДцдкЕуB(x1,y1),ЪЙЕУЙ§ЕуBЕФЧаЯпгыСНзјБъжсЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЕШгк .ШєДцдк,ЧыЧѓГіЕуBЕФзјБъ;ШєВЛДцдк,ЧыЫЕУїРэгЩ.
.ШєДцдк,ЧыЧѓГіЕуBЕФзјБъ;ШєВЛДцдк,ЧыЫЕУїРэгЩ.
(1) y=-1 (2) x2=4y (3) Дцдк ЕуBЕФзјБъЮЊ(2,1)Лђ(-2,1)ЃЌРэгЩМћНтЮі
ЁОНтЮіЁП(1)СНдВЕФАыОЖЖМЮЊ1,СНдВЕФдВаФЗжБ№ЮЊC1(0,-4),C2(0,2),
гЩЬтвтЕУ|CC1|=|CC2|,ПЩжЊдВаФCЕФЙьМЃЪЧЯпЖЮC1C2ЕФДЙжБЦНЗжЯп,C1C2ЕФжаЕуЮЊ(0,-1),жБЯпC1C2ЕФаБТЪВЛДцдк,ЙЪдВаФCЕФЙьМЃЪЧЯпЖЮC1C2ЕФДЙжБЦНЗжЯп,ЦфЗНГЬЮЊy=-1,МДдВCЕФдВаФЙьМЃLЕФЗНГЬЮЊy=-1.
(2)вђЮЊm=n,ЫљвдM(x,y)ЕНжБЯпy=-1ЕФОрРыгыЕНЕуF(0,1)ЕФОрРыЯрЕШ,ЙЪЕуMЕФЙьМЃQЪЧвдy=-1ЮЊзМЯп,вдЕуF(0,1)ЮЊНЙЕу,ЖЅЕудкдЕуЕФХзЮяЯп,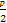 =1,МДp=2,Ыљвд,ЙьМЃQЕФЗНГЬЪЧx2=4y.
=1,МДp=2,Ыљвд,ЙьМЃQЕФЗНГЬЪЧx2=4y.
(3)МйЩшДцдкЕуBТњзуЬѕМў.гЩ(2)ЕУy=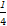 x2,y'=
x2,y'=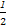 x,ЫљвдЙ§ЕуBЕФЧаЯпЕФаБТЪЮЊk=
x,ЫљвдЙ§ЕуBЕФЧаЯпЕФаБТЪЮЊk=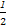 x1,
x1,
ЧаЯпЗНГЬЮЊy-y1=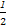 x1(x-x1).
x1(x-x1).
Сюx=0ЕУy=-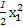 +y1,
+y1,
Сюy=0ЕУx=-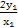 +x1.
+x1.
вђЮЊЕуBдкx2=4yЩЯ,Ыљвдy1=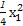 ,
,
ЙЪy=-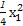 ,x=
,x=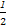 x1,
x1,
ЫљвдЧаЯпгыСНзјБъжсЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ
S=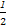 |x||y|=
|x||y|=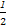 |
|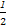 x1||-
x1||-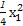 |=
|=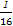 |
|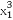 |,
|,
Ыљвд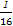 |
|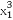 |=
|=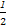 ,НтЕУ|x1|=2,
,НтЕУ|x1|=2,
Ыљвдx1=ЁР2.
ЕБx1=2ЪБ,y1=1,ЕБx1=-2ЪБ,y1=1,ЫљвдЕуBЕФзјБъЮЊ(2,1)Лђ(-2,1).

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ