题目内容
给出下列四个命题:
①已知a,b,m都是正数,且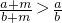 ,则a<b;
,则a<b;
②已知a、b、c成等比数列,a、x、b成等差数列,b、y、c也成等差数列,则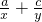 的值等于2;
的值等于2;
③函数y=tanx的图象关于点(kπ,0),(k∈Z)对称;
④关于x的不等式|x+1|+|x-3|≥m的解集为R,则m≤4;
其中为真命题的序号是________.
①②③④
分析:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数、数列和不等式的一些性质.
命题①根据a,b,m都是正数这一特点,两边同乘b(b+m);
命题②根据等比和等差中项的概念,得出各字母间的关系,然后同分代值即可;
命题③只需把点的坐标代入函数解析式验证;
命题④若分段求解较为繁杂,可利用绝对值的几何意义求出不等式左侧的范围.
解答:①∵a,b,m都是正数,则由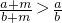 ?b(a+m)>a(b+m),∴ab+bm>ab+am,即bm>am,则a<b,故命题①正确.
?b(a+m)>a(b+m),∴ab+bm>ab+am,即bm>am,则a<b,故命题①正确.
②由a、b、c成等比数列,a、x、b成等差数列,b、y、c也成等差数列,得b2=ac,2x=a+b,2y=b+c,后两式相乘得4xy=ab+b2+ab+bc=ab+2ac+bc,
所以 =
= =
= =
= =
= ,所以命题②正确.
,所以命题②正确.
③∵y=tankπ=0,函数y=tanx的图象关于点(kπ,0),(k∈Z)对称,所以命题③正确.
④令y=|x+1|+|x-3|,根据绝对值的几何意义,|x+1|+|x-3|可看作数轴上的动点X到两实数-1和2所对应两定点的距离,所以ymin=4,
那么要使不等式|x+1|+|x-3|≥m的解集为R,则m≤4,所以命题④正确.
故答案为①②③④.
点评:对于命题②的计算,通分后的分子采用了整体代换,使运算过程得到了简化;
命题④中运用了绝对值的几何意义,含绝对值不等式的求解,有时考虑到绝对值的几何意义,可使解题过程大大简化.
分析:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数、数列和不等式的一些性质.
命题①根据a,b,m都是正数这一特点,两边同乘b(b+m);
命题②根据等比和等差中项的概念,得出各字母间的关系,然后同分代值即可;
命题③只需把点的坐标代入函数解析式验证;
命题④若分段求解较为繁杂,可利用绝对值的几何意义求出不等式左侧的范围.
解答:①∵a,b,m都是正数,则由
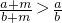 ?b(a+m)>a(b+m),∴ab+bm>ab+am,即bm>am,则a<b,故命题①正确.
?b(a+m)>a(b+m),∴ab+bm>ab+am,即bm>am,则a<b,故命题①正确.②由a、b、c成等比数列,a、x、b成等差数列,b、y、c也成等差数列,得b2=ac,2x=a+b,2y=b+c,后两式相乘得4xy=ab+b2+ab+bc=ab+2ac+bc,
所以
 =
= =
= =
= =
= ,所以命题②正确.
,所以命题②正确.③∵y=tankπ=0,函数y=tanx的图象关于点(kπ,0),(k∈Z)对称,所以命题③正确.
④令y=|x+1|+|x-3|,根据绝对值的几何意义,|x+1|+|x-3|可看作数轴上的动点X到两实数-1和2所对应两定点的距离,所以ymin=4,
那么要使不等式|x+1|+|x-3|≥m的解集为R,则m≤4,所以命题④正确.
故答案为①②③④.
点评:对于命题②的计算,通分后的分子采用了整体代换,使运算过程得到了简化;
命题④中运用了绝对值的几何意义,含绝对值不等式的求解,有时考虑到绝对值的几何意义,可使解题过程大大简化.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目