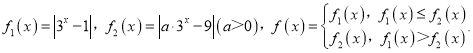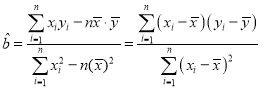题目内容
【题目】随着创新驱动发展战略的不断深入实施,高新技术企业在科技创新和经济发展中的带动作用日益凸显,某能源科学技术开发中心拟投资开发某新型能源产品,估计能获得![]() 万元的投资收益,现准备制定一个对科研课题组的奖励议案:奖金
万元的投资收益,现准备制定一个对科研课题组的奖励议案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,奖金不超过
(单位:万元)的增加而增加,奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .(即:设奖励方案函数模拟为
.(即:设奖励方案函数模拟为![]() 时,则公司对函数模型的基本要求是:当
时,则公司对函数模型的基本要求是:当![]() 时,①
时,①![]() 是增函数;②
是增函数;②![]() 恒成立;③
恒成立;③![]() 恒成立.)
恒成立.)
(1)现有两个奖励函数模型:(I)![]() ;(II)
;(II)![]() .试分析这两个函数模型是否符合公司要求?
.试分析这两个函数模型是否符合公司要求?
(2)已知函数![]() 符合公司奖励方案函数模型要求,求实数
符合公司奖励方案函数模型要求,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 函数(I)不符合公司要求;(II)模型符合公司要求;(2) ![]()
【解析】
(1)分别判断两个函数模型是否满足三个条件即可.
(2)由题意得函数![]() 满足三个条件,利用函数的单调性、均值不等式可求得
满足三个条件,利用函数的单调性、均值不等式可求得![]() 的取值范围.
的取值范围.
(1)对于函数模型(I):因为![]() ,即函数(I)不符合条件③,
,即函数(I)不符合条件③,
所以函数模型(I)![]() 不符合公司要求.
不符合公司要求.
对于函数模型(II):当![]() 时,
时,![]() 是增函数,
是增函数,
且![]() ,所以
,所以![]() 恒成立.
恒成立.
设![]() ,因为
,因为![]() ,
,
所以当![]() 时,
时,![]() .
.
所以![]() 恒成立.
恒成立.
所以函数模型(II)![]() 符合公司要求.
符合公司要求.
(2)因为![]() ,所以函数
,所以函数![]() 满足条件①.
满足条件①.
由函数![]() 满足条件②得:
满足条件②得:![]() ,所以
,所以![]() .
.
由函数![]() 满足条件③得:
满足条件③得:![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,因为
恒成立,因为![]() ,
,
当且仅当![]() 时等号成立,所以
时等号成立,所以![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】学校从参加高一年级期中考试的学生中抽出50名学生,并统计了她们的数学成绩(成绩均为整数且满分为150分),得到的样本频率分布表如下:
分组 | 频数 | 频率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 14 | 0.28 |
| 15 | 0.30 |
|
|
|
| 4 | 0.08 |
合计 |
|
|
(1)在给出的样本频率分布表中,求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计成绩在120分以上(含120分)学生的比例;
(3)抽取的50名学生中,为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在![]() 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在![]() 中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为135分,求甲、乙两同学恰好被安排在同一小组的概率.
中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为135分,求甲、乙两同学恰好被安排在同一小组的概率.