Question

已知函数f（x）=lnx，g(x)=

1

2

x2+a（a为常数），若直线l与y=f（x）和y=g（x）的图象都相切，且l与y=f（x）的图象相切于定点P（1，f（1））．
（1）求直线l的方程及a的值；
（2）当k∈R时，讨论关于x的方程f（x²+1）-g（x）=k的实数解的个数．

Answer 1

分析：（1）先利用导数求出函数f（x）=lnx在定点P（1，f（1））处的切线斜率，从而得到直线l的方程，再根据直线l与y=g（x）相切，联立方程组，消去y，根据△=0可求出a的值；
（2）令h（x）=f（x²+1）-g（x），然后利用导数研究函数的单调性，得到函数的极值，画出草图，讨论k的取值范围，从而判别方程f（x²+1）-g（x）=k的实数解的个数．

解答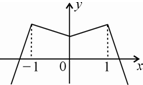：解：（1）f′(x)=

1

x

，∴f'（1）=1．∴切点为（1，0）．
∴l的解析式为y=x-1．（2分）
又l与y=g（x）相切，
∴

y=x-1 y= 1 2 x2+a

⇒x2-2x+2a+2=0
△=（-2）²-4（2a+2）=0⇒a=-

1

2

（5分）
（2）令h(x)=f(x2+1)-g(x)=ln(x2+1)-

1

2

x2+

1

2

∴h′(x)=

2x

x2+1

-x=

-x3+x

x2+1

=-

x(x+1)(x-1)

x2+1

（7分）
令h'（x）=0⇒x₁=0，x_2，3=±1．

x	（-∞，-1）	-1	（-1，0）	0	（0，1）	1	（1，+∞）
h'（x）	+	0	-		+		-
h（x）	↗	极大值ln2	↘	极小值 1 2	↗	极大值ln2	↘

1°k∈（ln2，+∞）时，方程无解．
2°当k=ln2时，方程有2解．
3°当

1

2

＜k＜ln2，方程有4解
.4°当k=

1

2

时，方程有3解．
5°当k＜

1

2

时，方程有2解．（13分）

点评：本题主要考查了利用导数研究曲线上某点切线方程，以及利用导数研究函数的极值，同时考查了画图能力以及分类讨论的数学思想，属于中档题．