题目内容
已知函数 (
(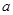 、
、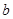 为常数,
为常数,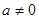 ,
,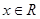 )在
)在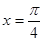 处
处
取得最小值,则函数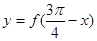 是( )
是( )
A.偶函数且它的图象关于点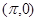 对称 对称 | B.偶函数且它的图象关于点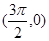 对称 对称 |
C.奇函数且它的图象关于点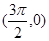 对称 对称 | D.奇函数且它的图象关于点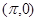 对称 对称 |
D
解析考点:函数y=Asin(ωx+φ)的图象变换.
分析:先对函数f(x)运用三角函数的辅角公式进行化简求出最小正周期,根据正弦函数的最值和取得最值时的x的值可求出函数 的解析式,进而得到答案.
的解析式,进而得到答案.
解:已知函数f(x)=asinx-bcosx(a、b为常数,a≠0,x∈R),
∴f(x)= sin(x-φ)的周期为2π,若函数在x=
sin(x-φ)的周期为2π,若函数在x= 处取得最小值,不妨设f(x)=sin(x-
处取得最小值,不妨设f(x)=sin(x- ),
),
则函数y=f( -x)=sin(
-x)=sin( -x-
-x- )=-sinx,
)=-sinx,
所以y=f( -x)是奇函数且v的图象关于点(π,0)对称,
-x)是奇函数且v的图象关于点(π,0)对称,
故选D.
点评:本题主要考查辅角公式、三角函数的奇偶性和对称性.对于三角函数的基本性质要熟练掌握,这是解题的根本.

练习册系列答案
相关题目