题目内容
在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足①![]() , ②
, ②![]() =
= ![]() =
= ![]() ③
③![]() ∥
∥![]()
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(![]() , 0) ,已知
, 0) ,已知![]() ∥
∥![]() ,
,
![]() ∥
∥![]() 且
且![]() ·
·![]() = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
(1) ![]() (x≠0)(2) Smax = 2 , Smin =
(x≠0)(2) Smax = 2 , Smin = ![]() 。
。
解析:
(1)设C ( x , y ), ![]()
![]() ,由①知
,由①知![]() ,
,
![]() G为△ABC的重心 ,
G为△ABC的重心 , ![]() G(
G(![]() ,
,![]() )
)
由②知M是△ABC的外心,![]() M在x轴上
M在x轴上
由③知M(![]() ,0),
,0),
由![]() 得
得![]()
化简整理得:![]() (x≠0 )
(x≠0 )
(2)F(![]() ,0 )恰为
,0 )恰为![]() 的右焦点
的右焦点
设PQ的斜率为k≠0且k≠±![]() ,则直线PQ的方程为y = k ( x -
,则直线PQ的方程为y = k ( x -![]() )
)
由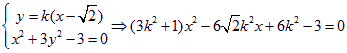
设P(x1 , y1) ,Q (x2 ,y2 ) 则x1 + x2 = ![]() , x1·x2 =
, x1·x2 =![]()
|
= ![]() ·
·![]()
= ![]()
![]() RN⊥PQ,把k换成
RN⊥PQ,把k换成![]() 得 | RN
得 | RN
![]() S =
S =![]() | PQ | · | RN |
| PQ | · | RN |
=![]()
=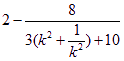 )
)
![]()
![]() ≥2 ,
≥2 , ![]() ≥16
≥16
![]() ≤ S < 2 , (当 k = ±1时取等号)
≤ S < 2 , (当 k = ±1时取等号)
又当k不存在或k = 0时S = 2
综上可得 ![]() ≤ S ≤ 2
≤ S ≤ 2
![]() Smax = 2 , Smin =
Smax = 2 , Smin = ![]()
|

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目