题目内容

椭圆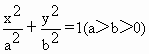的左、右焦点分别为F1、F2，过F1的直线l与椭圆交于A、B两点．

(1)如果点A在圆x2＋y2＝c2(c为椭圆的半焦距)上，且|F1A|＝c，求椭圆的离心率；

(2)若函数的图象，无论m为何值时恒过定点(b，a)，求的取值范围．

答案：
解析：

　　解：(1)∵点A在圆，

　　

　　由椭圆的定义知：|AF1|+|AF2|＝2a，

　　

　　(2)∵函数

　　∴

　　点F1(－1，0)，F2(1，0)，

　　①若，

　　∴

　　②若AB与x轴不垂直，设直线AB的斜率为k，则AB的方程为y＝k(x+1)

　　由　(*)

　　方程(*)有两个不同的实根．

　　设点A(x1，y1)，B(x2，y2)，则x1，x2是方程(*)的两个根

　　

　　

　　

　　

　　

　　由①②知


练习册系列答案
相关题目
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
3
，以原点为圆心，椭圆短半轴长为半径的圆与y=x+2相切．
（1）求a与b；
（2）设该椭圆的左、右焦点分别为F1和F2，直线l过F2且与x轴垂直，动直线l2与y轴垂直，l2交l1与点P．求PF1线段垂直平分线与l2的交点M的轨迹方程，并说明曲线类型．
给出以下5个命题：
①曲线x2-（y-1）2=1按
a
=(1，-2)平移可得曲线（x+1）2-（y-3）2=1；
②设A、B为两个定点，n为常数，|
PA
|-|
PB
|=n，则动点P的轨迹为双曲线；
③若椭圆的左、右焦点分别为F1、F2，P是该椭圆上的任意一点，延长F1P到点M，使|F2P|=|PM|，则点M的轨迹是圆；
④A、B是平面内两定点，平面内一动点P满足向量
AB
与
AP
夹角为锐角θ，且满足 |
PB
| |
AB
| +
PA
•
AB
=0，则点P的轨迹是圆（除去与直线AB的交点）；
⑤已知正四面体A-BCD，动点P在△ABC内，且点P到平面BCD的距离与点P到点A的距离相等，则动点P的轨迹为椭圆的一部分．
其中所有真命题的序号为
 
．
已知椭圆的左、右焦点分别为F1，F2，椭圆的离心率为
1
2
且经过点P(1，
3
2
)．M为椭圆上的动点，以M为圆心，MF2为半径作圆M．
（1）求椭圆C的标准方程；
（2）若圆M与y轴有两个交点，求点M横坐标的取值范围；
（3）是否存在定圆N，使得圆N与圆M相切？若存在．求出圆N的方程；若不存在，说明理由．
（2011•重庆一模）给出以下4个命题：
①曲线x2-（y-1）2=1按
a
=（1，-2）平移可得曲线（x+1）2-（y-3）2=1；
②若|x-1|+|y-1|≤1，则使x-y取得最小值的最优解有无数多个；
③设A、B为两个定点，n为常数，|
PA
|-|
PB
|=n，则动点P的轨迹为双曲线；
④若椭圆的左、右焦点分别为F1、F2，P是该椭圆上的任意一点，延长F1P到点M，使|F2P|=|PM|，则点M的轨迹是圆．
其中所有真命题的序号为
②④
②④
．

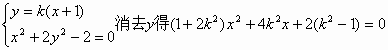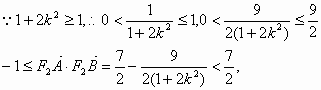
（本题12分）已知椭圆的左、右焦点分别为F1、F2，其中F2也是抛物线的焦点，M是C1与C2在第一象限的交点，且  

（I）求椭圆C1的方程；  （II）已知菱形ABCD的顶点A、C在椭圆C1上，顶点B、D在直线上，求直线AC的方程。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网