题目内容
不等式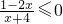 的解集为________.
的解集为________.
(-∞,-4)∪[ ,+∞)
,+∞)
分析:把原不等式化为2x-1与x+4相乘的式子,根据两数相乘同号得负,分类讨论2x-1与x+4的同时为正或同时为负,即可得到原不等式的解集.
解答:原不等式化为:(2x-1)(x+4)≥0,
即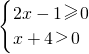 或
或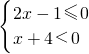 ,
,
解得:x 或x<-4,
或x<-4,
则原不等式的解集为:(-∞,-4)∪[ ,+∞).
,+∞).
故答案为:(-∞,-4)∪[ ,+∞)
,+∞)
点评:此题考查了其他不等式的解法,考查了分类讨论及转化的数学思想,是一道基础题.
 ,+∞)
,+∞)分析:把原不等式化为2x-1与x+4相乘的式子,根据两数相乘同号得负,分类讨论2x-1与x+4的同时为正或同时为负,即可得到原不等式的解集.
解答:原不等式化为:(2x-1)(x+4)≥0,
即
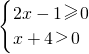 或
或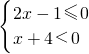 ,
,解得:x
 或x<-4,
或x<-4,则原不等式的解集为:(-∞,-4)∪[
 ,+∞).
,+∞).故答案为:(-∞,-4)∪[
 ,+∞)
,+∞)点评:此题考查了其他不等式的解法,考查了分类讨论及转化的数学思想,是一道基础题.

练习册系列答案
相关题目
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)