题目内容
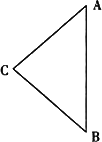
 正三角形ABC,点M,N,P分别为AB,BC,AC中点,沿MN,MP,NP折起,使A,B,C三点重合后为Q,则折起后二面角Q-MN-P的余弦值为( )
正三角形ABC,点M,N,P分别为AB,BC,AC中点,沿MN,MP,NP折起,使A,B,C三点重合后为Q,则折起后二面角Q-MN-P的余弦值为( )分析:利用折起后的三棱锥是正四面体的性质、余弦定理及二面角的定义即可得出.
解答:解:如图所示:折起的三棱锥Q-MNP为正四面体.取MN的中点O,连接QO、OP,则OQ⊥MN,OP⊥MN,
∴∠POQ为二面角Q-MN-P的平面角.
不妨设MN=2,则PQ=2,OP=OQ=
.
在△OPQ中,由余弦定理可得:cos∠POQ=
=
.
∴折起后二面角Q-MN-P的余弦值为
.
故选A.
∴∠POQ为二面角Q-MN-P的平面角.

不妨设MN=2,则PQ=2,OP=OQ=
| 3 |
在△OPQ中,由余弦定理可得:cos∠POQ=
(
| ||||
2×
|
| 1 |
| 3 |
∴折起后二面角Q-MN-P的余弦值为
| 1 |
| 3 |
故选A.
点评:熟练掌握正四面体的性质、余弦定理及二面角的定义是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
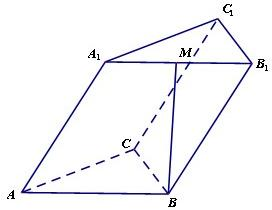 已知斜三棱柱ABC-A1B1C1的底面是正三角形,侧面ABB1A1是边长为2的菱形,且∠A1AB=60°,M是A1B1的中点,MB⊥AC.
已知斜三棱柱ABC-A1B1C1的底面是正三角形,侧面ABB1A1是边长为2的菱形,且∠A1AB=60°,M是A1B1的中点,MB⊥AC.