题目内容
已知集合M={P|P是棱长为1的正方体ABCD-A1B1C1D1表面上的点，且AP=| 2 |
分析：要使且AP=
，即在三个平面BC1，A1C1，CD1得到三条圆弧，圆弧的长是四分之一个圆，半径是1，最后由弧长公式求得 这三条曲线的长度和即可．
| 2 |
解答：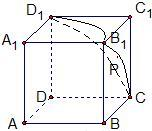
解：如图 集合M中所有点的轨迹是三段相等圆弧，圆弧的长是四分之一个圆，半径是1，
∴这条轨迹的长度是：3×
=
故答案为
．
解：如图 集合M中所有点的轨迹是三段相等圆弧，圆弧的长是四分之一个圆，半径是1，∴这条轨迹的长度是：3×
| 2π |
| 4 |
| 3π |
| 2 |
故答案为
| 3π |
| 2 |
点评：本题考查直角正方体中的线段的关系，弧长公式的应用．本题中这条曲线是以A为球心，以 1为半径的球与正方体表面的交线．
练习册系列答案
阅读快车系列答案
相关题目
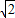}，则集合M中所有点的轨迹的长度是 ．