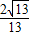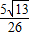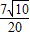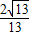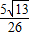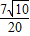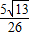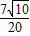Question

两直线3x+y-3=0与6x+my+1=0平行，则它们之间的距离为（　　）

• A、4
• B、

  2 13

  13

• C、

  5 13

  26

• D、

  7 10

  20

Answer 1

分析：根据两直线平行（与y轴平行除外）时斜率相等，得到m的值，然后从第一条直线上取一点，求出这点到第二条直线的距离即为平行线间的距离．

解答：解：根据两直线平行得到斜率相等即-3=-

6

m

，解得m=2，则直线为6x+2y+1=0，
取3x+y-3=0上一点（1，0）求出点到直线的距离即为两平行线间的距离，
所以d=

|6+1|

62+22

=

7 10

20

．
故选D

点评：此题是一道基础题，要求学生会把两条直线间的距离转化为点到直线的距离．