题目内容
已知n是不小于3的正整数,an=| n |
 |
| k=1 |
| C | k n |
| n |
 |
| k=1 |
| C | k n |
(1)求an,bn;
(2)设cn=
| an |
| bn |
| n |
 |
| k=1 |
分析:(1)由于an,bn是以和式出现,而且与组合数有关,借助于kCnk=nCn-1k-1,可进行转化,从而求出数列的通项公式;
(2)由(1)知cn=
=
,∴ckck+1=4(
-
),从而利用裂项求和法求和,故可证.
(2)由(1)知cn=
| an |
| bn |
| 2 |
| n+1 |
| 1 |
| k+1 |
| 1 |
| k+2 |
解答:解:(1)an=
k
=
+2
+…+n
,
因为kCnk=nCn-1k-1,所以an=nCn-10+nCn-11+…+nCn-1n-1=n(Cn-10+Cn-11+…+Cn-1n-1)=n•2n-1.…3分
因为k2Cnk=k•kCnk=k•nCn-1k-1,而kCn-1k-1=(k-1)Cn-1k-1+Cn-1k-1=(n-1)Cn-2k-2+Cn-1k-1(k≥2),
所以,bn=
k2
=n+
[n(n-1)
+n
]=n+n(n-1)
+n
=n(n-1)•2n-2+n•2n-1=n(n+1)•2n-2.
(2)cn=
=
=
,
所以
(ckck+1)=4
(
-
)=4(
-
)<2.
| n |
 |
| k=1 |
| C | k n |
| C | 1 n |
| C | 2 n |
| C | n n |
因为kCnk=nCn-1k-1,所以an=nCn-10+nCn-11+…+nCn-1n-1=n(Cn-10+Cn-11+…+Cn-1n-1)=n•2n-1.…3分
因为k2Cnk=k•kCnk=k•nCn-1k-1,而kCn-1k-1=(k-1)Cn-1k-1+Cn-1k-1=(n-1)Cn-2k-2+Cn-1k-1(k≥2),
所以,bn=
| n |
 |
| k=1 |
| C | k n |
| n |
 |
| k=2 |
| C | k-2 n-2 |
| C | k-1 n-1 |
| n |
 |
| k=2 |
| C | k-2 n-2 |
| n |
 |
| k=2 |
| C | k-1 n-1 |
=n(n-1)•2n-2+n•2n-1=n(n+1)•2n-2.
(2)cn=
| an |
| bn |
| n•2n-1 |
| n(n+1)•2n-2 |
| 2 |
| n+1 |
所以
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
点评:本题主要考查数列通项的求解及裂项求和法,同时考查了组合数的性质,有一定的综合性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
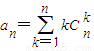 ,
,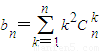 .
.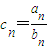 ,求证:
,求证: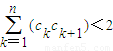 .
. ,
, .
. ,求证:
,求证: .
.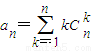 ,
,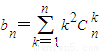 .
.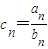 ,求证:
,求证: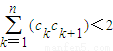 .
.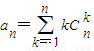 ,
,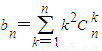 .
.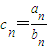 ,求证:
,求证: .
.