题目内容
若 ,
, 是非零向量,“
是非零向量,“ ⊥
⊥ ”是“函数
”是“函数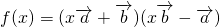 为一次函数”的
为一次函数”的
- A.充分而不必要条件
- B.必要不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
B
分析:先判别必要性是否成立,根据一次函数的定义,得到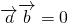 ,则
,则 成立,再判断充分性是否成立,由
成立,再判断充分性是否成立,由 ,不能推出函数为一次函数,因为
,不能推出函数为一次函数,因为 时,函数是常数,而不是一次函数.
时,函数是常数,而不是一次函数.
解答: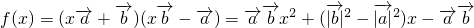 ,
,
如 ,则有
,则有 ,
,
如果同时有 ,则函数恒为0,不是一次函数,因此不充分,
,则函数恒为0,不是一次函数,因此不充分,
而如果f(x)为一次函数,则 ,因此可得
,因此可得 ,故该条件必要.
,故该条件必要.
故答案为B.
点评:此题考查必要条件、充分条件与充要条件的判别,同时考查平面向量的数量积的相关运算.
分析:先判别必要性是否成立,根据一次函数的定义,得到
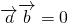 ,则
,则 成立,再判断充分性是否成立,由
成立,再判断充分性是否成立,由 ,不能推出函数为一次函数,因为
,不能推出函数为一次函数,因为 时,函数是常数,而不是一次函数.
时,函数是常数,而不是一次函数.解答:
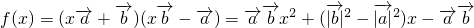 ,
,如
 ,则有
,则有 ,
,如果同时有
 ,则函数恒为0,不是一次函数,因此不充分,
,则函数恒为0,不是一次函数,因此不充分,而如果f(x)为一次函数,则
 ,因此可得
,因此可得 ,故该条件必要.
,故该条件必要.故答案为B.
点评:此题考查必要条件、充分条件与充要条件的判别,同时考查平面向量的数量积的相关运算.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 、
、 ,下列命题正确的是( )
,下列命题正确的是( )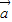 •
•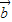 =0,则|
=0,则|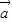 |=0,|
|=0,|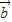 |=0
|=0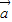 2•
2•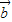 2
2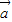 |=|
|=| |=1,则
|=1,则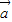 =±
=±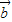
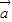 、
、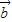 是非零向量,且
是非零向量,且 ⊥
⊥ ,则|
,则|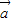 +
+ |=|
|=|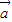 -
-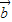 |
| ,
, 是非零向量,且
是非零向量,且 ⊥
⊥ ,|
,| |≠|
|≠| |,则函数f(x)=(x
|,则函数f(x)=(x +
+ )(x
)(x -
- )是( )
)是( )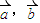 都是非零向量,且
都是非零向量,且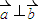 ,
,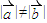 ,则函数
,则函数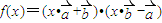 是( )
是( ) ,
, 是非零向量,且
是非零向量,且 ⊥
⊥ ,|
,| |≠|
|≠| |,则函数f(x)=(x
|,则函数f(x)=(x +
+ )(x
)(x -
- )是( )
)是( )