题目内容
已知α,β∈R,写出用cosα,cosβ,sinα,sinβ表示cos(α-β)的关系等式,并证明这个关系等式.
cos(α-β)=cosαcosβ+sinαsinβ.-----(2分)
证明:如图,在平面直角坐标系xoy内作单位圆O,以Ox为始边作角α、β,它们的终边与单位圆的交点分别为A,B.
则
=(cosα,sinα),
=(cosβ,sinβ),
由向量数量积的定义,有
•
=|
|•|
|cos<
,
>=cos<
,
>,
由向量数量积的坐标表示,有
•
=cosαcosβ+sinαsinβ.
于是cos<
,
>=cosαcosβ+sinαsinβ.①------(7分)
对于任意的α、β,总可选取适当的整数k,使得 α-β=<
,
>+2kπ,或α-β=-<
,
>+2kπ,
故对于任意的α、β,总有 cos(α-β)=cos<
,
>成立,带入①式得,
对 α、β∈R,总有cos(α-β)=cosαcosβ+sinαsinβ 成立.------(12分)
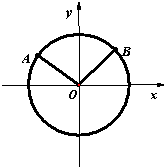
证明:如图,在平面直角坐标系xoy内作单位圆O,以Ox为始边作角α、β,它们的终边与单位圆的交点分别为A,B.
则
| OA |
| OB |
由向量数量积的定义,有
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
由向量数量积的坐标表示,有
| OA |
| OB |
于是cos<
| OA |
| OB |
对于任意的α、β,总可选取适当的整数k,使得 α-β=<
| OA |
| OB |
| OA |
| OB |
故对于任意的α、β,总有 cos(α-β)=cos<
| OA |
| OB |
对 α、β∈R,总有cos(α-β)=cosαcosβ+sinαsinβ 成立.------(12分)


练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
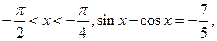 求值:
求值: (Ⅰ)
(Ⅰ)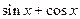 ;
;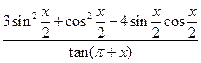 .
.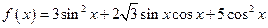 .
.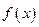 的周期和最大值;(Ⅱ)已知
的周期和最大值;(Ⅱ)已知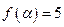 ,求
,求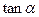 的值.
的值.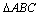 中,角
中,角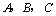 的对边分别是
的对边分别是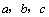 ,已知
,已知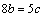 ,
,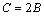 ,则
,则 ( ).
( ).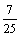
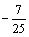
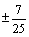
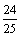
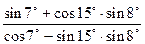 =___________.
=___________.