题目内容
已知函数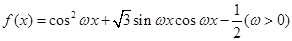 的最小正周期为
的最小正周期为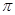 .
.
(I)求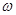 值及
值及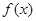 的单调递增区间;
的单调递增区间;
(II)在△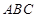 中,
中,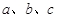 分别是三个内角
分别是三个内角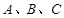 所对边,若
所对边,若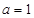 ,
,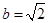 ,
,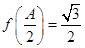 ,求
,求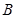 的大小.
的大小.
【答案】
(I)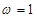 ;
;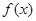 的单调递增区间为
的单调递增区间为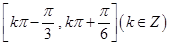 ;(II)
;(II)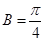 或
或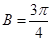 .
.
【解析】
试题分析:(I)由已知首先利用降幂扩角和倍角公式: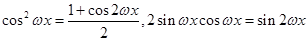 ,将函数
,将函数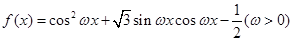 化为一个角的三角函数,利用公式
化为一个角的三角函数,利用公式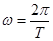 求
求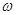 值,利用整体思想求
值,利用整体思想求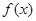 的单调递增区间;(II)由(I)
的单调递增区间;(II)由(I)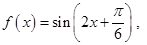 及已知
及已知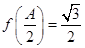 ,得
,得 ,由此可以求得
,由此可以求得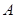 角.再利用正弦定理,得
角.再利用正弦定理,得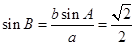 ,结合已知条件
,结合已知条件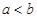 ,可求得角
,可求得角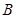 的大小.
的大小.
试题解析:(I)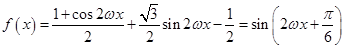 ,
, 最小正周期为
最小正周期为 ,
,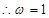 .
. 单调递增区间为
单调递增区间为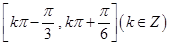 .
.
(II)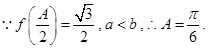
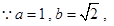 由正弦定理
由正弦定理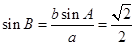 ,
,
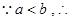
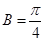 或
或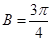 .
.
考点:1.三角恒等变换(倍角公式);2.三角函数的周期和单调性;3.正弦定理.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
.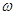 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.