题目内容
在等腰梯形ABCD中,AB∥CD,且AB>CD.设以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则e1•e2=分析:设AD=t,不妨设AB=2t,令∠DAB=θ,由余弦定理可求得 BD,由题意并结合椭圆、双曲线的定义,
求出a和 c的值,求出e1 和e2 的值,即可得到 e1•e2 的值.
求出a和 c的值,求出e1 和e2 的值,即可得到 e1•e2 的值.
解答:解:设AD=t,不妨设AB=2t,令∠DAB=θ,则由余弦定理可求得
BD=
=t
.在双曲线中,2a=DB-DA=t
-t,
c=t,
=
=
,∴e1=
.
在椭圆中,2a=BD+BC=t
+t,2c=DC,三角形BCD中,由余弦定理可得
BD2=BC2+DC2-2BD•DC cos(π-θ),即 t2(5-4cosθ)=t2+4c2+2t•2c•cosθ,
c=t(1-cosθ),e2=
=
=
.
∴e1•e2=
•
=1,
故答案为:1.
BD=
| t2+ 4t2-2t•2tcosθ |
| 5-4cosθ |
| 5-4cosθ |
c=t,
| c |
| a |
| t | ||||
|
| 2 | ||
|
| 2 | ||
|
在椭圆中,2a=BD+BC=t
| 5-4cosθ |
BD2=BC2+DC2-2BD•DC cos(π-θ),即 t2(5-4cosθ)=t2+4c2+2t•2c•cosθ,
c=t(1-cosθ),e2=
| c |
| a |
| t(1-cosθ) | ||||
|
| 2(1-cosθ) | ||
|
∴e1•e2=
| 2 | ||
|
| 2(1-cosθ) | ||
|
故答案为:1.
点评:本题考查椭圆的定义,以及简单性质的应用;双曲线的标准方程,以及双曲线的简单性质的应用,求出a 和c的值,
是解题的关键.
是解题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
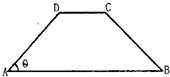 如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,| π |
| 2 |
| A、随着角度θ的增大,e1增大,e1e2为定值 |
| B、随着角度θ的增大,e1减小,e1e2为定值 |
| C、随着角度θ的增大,e1增大,e1e2也增大 |
| D、随着角度θ的增大,e1减小,e1e2也减小 |
 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为 在等腰梯形ABCD中,E、F分别是CD、AB中点,CD=2,AB=4,AD=BC=
在等腰梯形ABCD中,E、F分别是CD、AB中点,CD=2,AB=4,AD=BC= 如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式:
如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式: 如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是
如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是