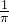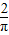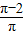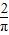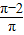题目内容
设D是由直线x=±π和y=±1所围成的矩形区域,E是D内函数y=cosx图象上方的点构成的区域,向D中随机投一点,则该点落入E(阴影部分)中的概率为( )
分析:由已知中D是图中所示的矩形区域,E是D内函数y=cosx图象上方的点构成的区域,分别求出D的面积和E的面积,代入几何概型概率计算公式,即可得到答案.
解答:解:∵矩形ABCD区域D的面积S=2×2π=4π
根据对称性可知图中阴影部分两处标注I的面积相等,两处标注II的面积相等,把x轴下方的I补到x轴上方的I,x轴下方的II补到x轴上方的II,
则阴影部分的面积与x轴上方的矩形面积相等,长宽分别为1,2π,即面积为1×2π=2π
∴由几何概率的求解公式可得,P=
=
故选C
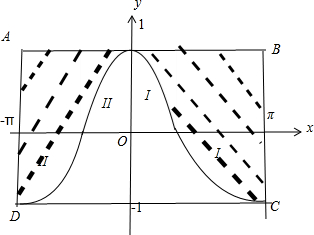
根据对称性可知图中阴影部分两处标注I的面积相等,两处标注II的面积相等,把x轴下方的I补到x轴上方的I,x轴下方的II补到x轴上方的II,
则阴影部分的面积与x轴上方的矩形面积相等,长宽分别为1,2π,即面积为1×2π=2π
∴由几何概率的求解公式可得,P=
| 2π |
| 4π |
| 1 |
| 2 |
故选C

点评:本题考查的知识点是几何概型,其中利用积分公式,根据余弦函数的对称性计算出阴影部分的面积是解答本题的关键.

练习册系列答案
相关题目