题目内容
设D、E、F分别是△ABC的三边BC、CA、AB上的点，且
=2
，
=2
，
=2
，则
+
+
与
（ ）
| DC |
| BD |
| CE |
| EA |
| AF |
| FB |
| AD |
| BE |
| CF |
| BC |
| A、反向平行 |
| B、同向平行 |
| C、互相垂直 |
| D、既不平行也不垂直 |
分析：根据向量的定必分点性质可分别表示出
=
=
+
，
=
+
，
=
+
，
然后三者相加即可得到答案．
| AD |
| ||||
| 1+2 |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
| BE |
| 1 |
| 3 |
| BC |
| 2 |
| 3 |
| BA |
| CF |
| 1 |
| 3 |
| CA |
| 2 |
| 3 |
| CB |
然后三者相加即可得到答案．
解答：解：由定比分点的向量式得：
=
=
+
，
=
+
，
=
+
，
以上三式相加得
+
+
=-
，
故选A
| AD |
| ||||
| 1+2 |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
| BE |
| 1 |
| 3 |
| BC |
| 2 |
| 3 |
| BA |
| CF |
| 1 |
| 3 |
| CA |
| 2 |
| 3 |
| CB |
以上三式相加得
| AD |
| BE |
| CF |
| 1 |
| 3 |
| BC |
故选A
点评：本题主要考查向量的共线定理和向量的定比分点问题．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
设D，E，F分别是△ABC的边BC，CA，AB上的点，且
＝2
，
＝2
，
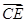＝2
，则
＋
＋
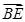与
( )