题目内容
已知函数 ,其中a∈R.
,其中a∈R.(Ⅰ)若函数f(x)为奇函数,求实数a的值;
(Ⅱ)若函数f(x)在区间[2,+∞)上单调递增,求实数a的取值范围.
【答案】分析:(Ⅰ)由题意可得f(-x)=-f(x),即 ,由此求得a的值.
,由此求得a的值.
(Ⅱ)根据f(x)在区间[2,+∞)上单调递增,可得 在[2,+∞)上恒成立,即
在[2,+∞)上恒成立,即 在[2,+∞)上恒成立,求得
在[2,+∞)上恒成立,求得 在[2,+∞)上的最
在[2,+∞)上的最
小值ymin=4,可得a≤4,验证知当a≤4满足条件.
解答:解:(Ⅰ)解:因为 是奇函数. 所以f(-x)=-f(x),其中x∈R且x≠0.…(2分)
是奇函数. 所以f(-x)=-f(x),其中x∈R且x≠0.…(2分)
即 ,其中x∈R且x≠0.
,其中x∈R且x≠0.
所以a=0.…(6分)
(Ⅱ)解: .…(8分)
.…(8分)
因为f(x)在区间[2,+∞)上单调递增,
所以 在[2,+∞)上恒成立,…(9分)
在[2,+∞)上恒成立,…(9分)
即 在[2,+∞)上恒成立,
在[2,+∞)上恒成立,
因为 在[2,+∞)上的最小值ymin=4,
在[2,+∞)上的最小值ymin=4,
所以 a≤4,验证知当a≤4时,f(x)在区间[2,+∞)上单调递增.…(13分)
点评:本题主要考查函数的奇偶性、单调性的应用,函数的恒成立问题,属于中档题.
 ,由此求得a的值.
,由此求得a的值.(Ⅱ)根据f(x)在区间[2,+∞)上单调递增,可得
 在[2,+∞)上恒成立,即
在[2,+∞)上恒成立,即 在[2,+∞)上恒成立,求得
在[2,+∞)上恒成立,求得 在[2,+∞)上的最
在[2,+∞)上的最小值ymin=4,可得a≤4,验证知当a≤4满足条件.
解答:解:(Ⅰ)解:因为
 是奇函数. 所以f(-x)=-f(x),其中x∈R且x≠0.…(2分)
是奇函数. 所以f(-x)=-f(x),其中x∈R且x≠0.…(2分)即
 ,其中x∈R且x≠0.
,其中x∈R且x≠0.所以a=0.…(6分)
(Ⅱ)解:
 .…(8分)
.…(8分)因为f(x)在区间[2,+∞)上单调递增,
所以
 在[2,+∞)上恒成立,…(9分)
在[2,+∞)上恒成立,…(9分)即
 在[2,+∞)上恒成立,
在[2,+∞)上恒成立,因为
 在[2,+∞)上的最小值ymin=4,
在[2,+∞)上的最小值ymin=4,所以 a≤4,验证知当a≤4时,f(x)在区间[2,+∞)上单调递增.…(13分)
点评:本题主要考查函数的奇偶性、单调性的应用,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.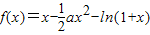 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.