题目内容

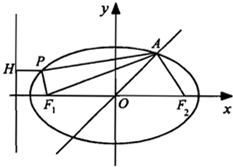
已知F1，F2为椭圆x2+6y2=36的两个焦点，P为椭圆上一点且PF1⊥PF2，则△F1PF2的面积是（　　）
A．36B．12C．6D．4
椭圆x2+6y2=36，所以a=6，b=
6
，c=
30
，
根据椭圆的定义，PF1+PF2=2a=10 ①
∵PF1⊥PF2，由勾股定理得，PF12+PF22=F1F22=4c2=4×（36-6）=120 ②
①2-②得2PF1×PF2=144-120=24
∴S△F1PF2=
1
2
×PF1×PF2=
1
2
×12=6
故选C．
练习册系列答案
相关题目
已知椭圆
x2
4
+
y2
3
=1，F1F2是它的两个焦点，P是这个椭圆上任意一点，那么当|PF1|•|PF2|取最大值时，P、F1、F2三点（　　）
A．共线
B．组成一个正三角形
C．组成一个等腰直角三角形
D．组成一个锐角三角形
若点P在椭圆x2+2y2=2上，F1、F2分别是椭圆的两焦点，且∠F1PF2=90°，则△F1PF2的面积是______．
已知椭圆的两个焦点分别为F1（0，-8），F2（0，8），且椭圆上一点到两个焦点的距离之和为20，则此椭圆的方程为______．
椭圆
x2
5
+
y2
4
=1的焦距是（　　）
A．1B．2C．4D．8
命题P“曲线sinα•x2+cosα•y2=1为焦点在y轴上的椭圆”，写出让命题P成立的一个充分条件______（请填写关于α的值或区间）
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为4，F1F2分别是椭圆C的左，右焦点，直线y=x与椭圆C在第一象限内的交点为A，△AF1F2的面积为2
6
，点P（x0，y0），是椭圆C上的动点w．
（1）求椭圆C的方程；
（2）若∠F1PF2为钝角，求点P的横坐标x0的取值范围；
（3）求
3
PF1+
2
PA的最小值．
AB是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的任意一条与x轴不垂直的弦，O是椭圆的中心，e为椭圆的离心率，M为AB的中点，则KAB•KOM的值为（　　）
A．e-1B．1-eC．e2-1D．1-e2
过直线l：y=x+9上的一点P作一个长轴最短的椭圆，使其焦点为F1（-3，0），F2（3，0），则椭圆的方程为（　　）
A．
x2
12
+
y2
3
=1		B．
x2
25
+
y2
16
=1
C．
x2
45
+
y2
36
=1		D．
x2
81
+
y2
72
=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网