题目内容
在x轴正向到y轴正向的角为60°的斜坐标系中，点A，B的坐标分别为A(-
，2)，B(
，2+2
)，则线段AB的长度为（ ）
| 3 |
| 3 |
| 3 |
A、2
| ||
B、2
| ||
| C、6 | ||
| D、3 |
分析：由已知中在x轴正向到y轴正向的角为60°的斜坐标系中，点A，B的坐标分别为A(-
，2)，B(
，2+2
)，我们取C点坐标为（
，2），则得到|AC|及|BC|的长，及∠
ACB=120°，根据余弦定理，易求出AB两个点之间的距离．
| 3 |
| 3 |
| 3 |
| 3 |
ACB=120°，根据余弦定理，易求出AB两个点之间的距离．
解答：解：∵A，B的坐标分别为A(-
，2)，B(
，2+2
)，
且x轴正向到y轴正向的角为60°
取C点坐标为（
，2）
故|AC|=2
，|BC|=2
则|AB|=
=
=6
故选C
| 3 |
| 3 |
| 3 |
且x轴正向到y轴正向的角为60°
取C点坐标为（
| 3 |
故|AC|=2
| 3 |
| 3 |
则|AB|=
| |AC|2+|BC|2-2|AC|•|BC| •cos120° |
=
| 12+12+12 |
故选C
点评：本题考查的知识点是两点间的距离公式，及余弦定理，其中找到坐标为（
，2）的C点，并分析出∠ACB=120°，是解答本题的关键．
| 3 |
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
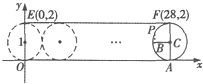如图，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在（0，1），此时圆上一点P的位置在（0，0），圆在x轴上沿正向滚动，则当圆滚动到圆心位于C（28，1）时，线段0P所在直线的方程为
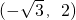，B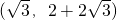
，则线段AB的长度为
