题目内容
【题目】已知函数![]() ,
,![]() .
.
(I)判断曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 的公共点个数;
的公共点个数;
(II)若函数![]() 有且仅有一个零点,求
有且仅有一个零点,求![]() 的值;
的值;
(III)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)详见解析;(II)![]() ;(III)
;(III)![]()
【解析】
(I)利用导函数求出函数![]() 在点
在点![]() ,
,![]() (1)
(1)![]() 处的切线方程,和函数
处的切线方程,和函数![]() 联立后由判别式分析求解公共点个数;
联立后由判别式分析求解公共点个数;
(II)写出函数![]() 表达式,由
表达式,由![]() 得到
得到![]() ,求函数
,求函数![]() 的最小值既是所要求的
的最小值既是所要求的![]() 的值;
的值;
(III)写出函数![]() 的表达式,构造辅助函数
的表达式,构造辅助函数![]() ,由原函数的极值点是其导函数的零点分析导函数对应方程根的情况,分离参数
,由原函数的极值点是其导函数的零点分析导函数对应方程根的情况,分离参数![]() 后构造新的辅助函数,求函数的最小值,然后分析当
后构造新的辅助函数,求函数的最小值,然后分析当![]() 大于函数最小值的情况,进一步求出当
大于函数最小值的情况,进一步求出当![]() 时的
时的![]() 的值,则答案可求.
的值,则答案可求.
解:(I)由![]() ,得
,得![]() ,
,
![]() (1)
(1)![]() ,又
,又![]() (1)
(1)![]() ,
,
![]() 曲线
曲线![]() 在点
在点![]() ,
,![]() (1)
(1)![]() 处的切线方程为
处的切线方程为![]() ,
,
代入![]() ,得
,得![]() ,
,
![]() 当
当![]() 或
或![]() 时,△
时,△![]() ,有两个公共点;
,有两个公共点;
当![]() 或
或![]() 时,△
时,△![]() ,有一个公共点;
,有一个公共点;
当![]() 时,△
时,△![]() ,没有公共点.
,没有公共点.
(II)![]() ,
,
由![]() ,得
,得![]() ,
,
令![]() ,
,![]()
![]() ,
,
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
因此,![]() (1)
(1)![]() .
.
(III)![]() ,
,
令![]() ,
,
![]() ,
,
即![]() 有两个不同的根
有两个不同的根![]() ,
,![]() ,
,
令![]()
![]()
![]() ,
,
且当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
当![]() 时,
时,
![]() ,
,
![]()
![]() ,
,
此时![]() .
.
即![]() 时,
时,
![]() .
.

【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不少于120分的有10人,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | 10 | ||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)在上述样本中从分数不少于120分的学生中,按照分层抽样的方法,抽到线上学习时间不少于5小时和线上学习时间不足5小时的学生共5名,若在这5名学生中随机抽取2人,求至少1人每周线上学习时间不足5小时的概率.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式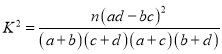 其中
其中![]() )
)