题目内容
如图,已知多面体 中,
中, ⊥平面
⊥平面 ,
, ⊥平面
⊥平面 ,
, ,
,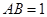 ,
, 为
为 的中点.
的中点.

(1)求证: ⊥平面
⊥平面 ;
;
(2)求二面角 的大小.
的大小.
【答案】
(1)根据题意,由于DE⊥平面ACD,AF 平面ACD,∴DE⊥AF,那么同时AF⊥CD,得到证明。
平面ACD,∴DE⊥AF,那么同时AF⊥CD,得到证明。
(2)
【解析】
试题分析:(Ⅰ)∵DE⊥平面ACD,AF 平面ACD,∴DE⊥AF.
平面ACD,∴DE⊥AF.
又∵AC=AD,F为CD中点,∴AF⊥CD,
因CD∩DE=D,∴AF⊥平面CDE.
(Ⅱ)取CE的中点Q,连接FQ,因为F为CD的中点,则FQ∥DE,故DE⊥平面ACD,∴FQ⊥平面ACD,又由(Ⅰ)可知FD,FQ,FA两两垂直,以O为坐标原点,建立如图坐标系,

则F(0,0,0),C( ,0,0),A(0,0,
,0,0),A(0,0, ),B(0,1,
),B(0,1, ),E(1,2,0).
),E(1,2,0).
设面ABC的法向量 ,则
,则
即 取.
取.
又平面ACD的一个法向量为 ,则
,则 即
即

∴ 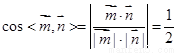 .
.
∴二面角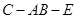 的大小为
的大小为 。
。
考点:线面的垂直以及二面角的平面角
点评:主要是考查了空间中线面的垂直的位置关系,以及二面角的求解,体现了向量法的运用,属于中档题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点. 中,
中,
 平面
平面 ,
,
 ,
, ,
,  ,
, 为
为 的中点
的中点

 ;
; 的体积.
的体积.