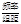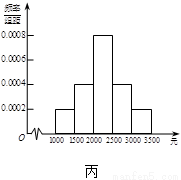题目内容
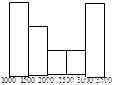
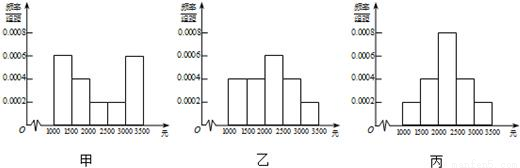
10、为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为
s1>s3>s2
.(用“>”连接)
分析:第二组数据是单峰的每一个小长方形的差别比较小,数字比较紧凑,得到第二组数据的波动最小,即标准差最小,第一组数据的两端数字较多,绝大部分数字都处在两端,而第三组数据绝大部分数字都在平均数左右,得到结果.
解答:解:根据三个频率分步直方图知,
第二组数据是单峰的每一个小长方形的差别比较小,数字比较紧凑,
∴第二组数据的波动最小,即标准差最小,
第一组数据的两端数字较多,绝大部分数字都处在两端,
而第三组数据绝大部分数字都在平均数左右,
∴第一组的标准差要大于第三组的标准差,
总上可知s1>s3>s2,
故答案为:s1>s3>s2,
第二组数据是单峰的每一个小长方形的差别比较小,数字比较紧凑,
∴第二组数据的波动最小,即标准差最小,
第一组数据的两端数字较多,绝大部分数字都处在两端,
而第三组数据绝大部分数字都在平均数左右,
∴第一组的标准差要大于第三组的标准差,
总上可知s1>s3>s2,
故答案为:s1>s3>s2,
点评:本题考查频率分步直方图,考查三组数据的标准差,考查标准差的意义,是比较几组数据的波动大小的量,考查读图,本题是一个基础题.

练习册系列答案
相关题目
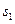 ,
, ,
,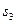 ,则它们的大小关系为 . (用“
,则它们的大小关系为 . (用“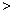 ”连接)
”连接)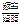
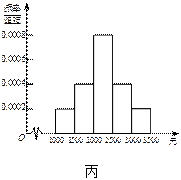



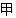

 ,
,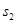 ,
,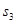 ,则它们的大小关系为
. (用“
,则它们的大小关系为
. (用“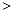 ”连接)
”连接)