题目内容
已知m,n是两条不重合的直线,α,β是两个不重合的平面,给出下列命题:
(1)若m⊥α,n⊥β且m⊥n,则α⊥β;
(2)若m∥α,n∥β且m∥n,则α∥β;
(3)若m⊥α,n∥β且m⊥n,则α⊥β;
(4)若m⊥α,n∥β且m∥n,则α∥β.
其中正确命题的个数是( )
(1)若m⊥α,n⊥β且m⊥n,则α⊥β;
(2)若m∥α,n∥β且m∥n,则α∥β;
(3)若m⊥α,n∥β且m⊥n,则α⊥β;
(4)若m⊥α,n∥β且m∥n,则α∥β.
其中正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
分析:对于(1)已知m,n是两条不重合的直线,α,β是两个不重合的平面,又已知m⊥α,n⊥β且m⊥n,可以看成m是平面α的法向量,n是平面β的法向量即可;
对于(2)已知m,n是两条不重合的直线,α,β是两个不重合的平面,又m∥α,n∥β且m∥n,则α∥β,画图即可判断;
对于(3)已知m,n是两条不重合的直线,α,β是两个不重合的平面,又m⊥α,n∥β且m⊥n,画图可以加以判断;
对于(4)已知m,n是两条不重合的直线,α,β是两个不重合的平面,又若m⊥α,n∥β且m∥n,则α∥β,画图即可.
对于(2)已知m,n是两条不重合的直线,α,β是两个不重合的平面,又m∥α,n∥β且m∥n,则α∥β,画图即可判断;
对于(3)已知m,n是两条不重合的直线,α,β是两个不重合的平面,又m⊥α,n∥β且m⊥n,画图可以加以判断;
对于(4)已知m,n是两条不重合的直线,α,β是两个不重合的平面,又若m⊥α,n∥β且m∥n,则α∥β,画图即可.
解答:解:(1)利用当两个平面的法向量互相垂直时,这两个平面垂直,可以知道(1)正确;
(2)由题意画出反例图为:
有图符合题中一切条件但两平面相交,故(2)错;
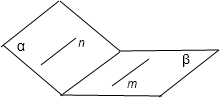
(3)由题意话反例图为:
此图符合题中的条件,但α∥β,所以(3)错;
(4)因为
?n⊥α,又因为n∥β,利用线面平行的性质定理可知总可以在β面内作l使得l∥n,所以l⊥α,l?β,利用面面垂直的判定定理可以知道α⊥β,故(4)正确.
故选C.
(2)由题意画出反例图为:
有图符合题中一切条件但两平面相交,故(2)错;

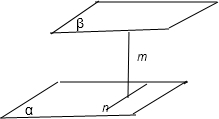
(3)由题意话反例图为:

此图符合题中的条件,但α∥β,所以(3)错;
(4)因为
|
故选C.
点评:此题考查了线面垂直,线面平行,面面垂直,面面平行等判定及性质,还考查了学生对于问题中已知条件的重组的能力即理解题意能力.

练习册系列答案
相关题目