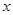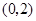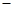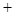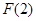题目内容
(本小题满分12分)设 ,
, .
.
(1)令 ,求
,求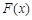 在
在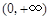 内的极值;
内的极值;
(2)求证:当 时,恒有
时,恒有 .
.
【答案】
.(1)解:根据求导法则有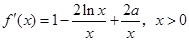 ,
,
故 ,
,
于是 ,
,
列表如下:
|
|
|
2 |
|
|
|
|
0 |
|
|
|
↘ |
极小值 |
↗ |
所以, 在
在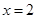 处取得极小值
处取得极小值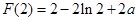 .
.
(2)证明:由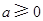 知,
知, 的极小值
的极小值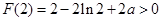 .
.
于是由上表知,对一切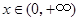 ,恒有
,恒有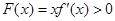 .
.
从而当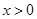 时,恒有
时,恒有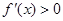 ,故
,故 在
在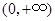 内单调增加.
内单调增加.
所以当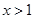 时,
时, ,即
,即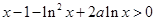 .
.
故当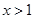 时,恒有
时,恒有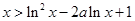 .
.
【解析】略

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目