题目内容
设关于x的不等式
<0的解集为S,且3∈S,4∉S,则实数a的取值范围为( )
| ax-1 |
| x2-a |
分析:由已知中关于x的不等式
<0的解集为S,且3∈S,4∉S,将3,4分别代入可以构造一个关于a的不等式,解不等式即可求出实数a的取值范围.
| ax-1 |
| x2-a |
解答:解:∵关于x的不等式
<0的解集为S,
若3∈S,则
<0,解得a∈(-∞,
)∪(9,+∞)
若4∉S,则16-a=0,或
≥0,解得a∈[
,16]
∵[(-∞,
)∪(9,+∞)]∪[
,16]=[
,
)∪(9,16]
故实数a的取值范围为[
,
)∪(9,16]
故选C
| ax-1 |
| x2-a |
若3∈S,则
| 3a-1 |
| 9-a |
| 1 |
| 3 |
若4∉S,则16-a=0,或
| 4a-1 |
| 16-a |
| 1 |
| 4 |
∵[(-∞,
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
故实数a的取值范围为[
| 1 |
| 4 |
| 1 |
| 3 |
故选C
点评:本题考查的知识点是分式不等式的解法,元素与集合关系的判定,其中根据已知条件构造关于a的不等式是解答本题的关键,本题易忽略4∉S时,包括4使分母为0的情况,而错解为[
,
)∪(9,16)
| 1 |
| 4 |
| 1 |
| 3 |

练习册系列答案
相关题目
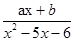 >0的解集为________.
>0的解集为________.