题目内容
已知⊙O:x2+y2=4交x轴的负半轴于点P,直线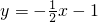 与⊙O另一交点为点Q,点S为圆上任一点.
与⊙O另一交点为点Q,点S为圆上任一点.
(1)求弦PQ的长;
(2)当点S将上半圆分成1:2两部分圆弧时,求直线PS的方程;
(3)求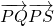 的最大值.
的最大值.
解:(1)直线方程为x+2y+2=0,则点O到直线的距离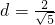
∴弦PQ=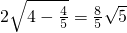 (4分)
(4分)
(2)由题意得: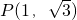 或
或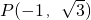 ,(6分)
,(6分)
直线PS的方程为 或
或 (8分)
(8分)
(3)∵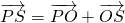
∴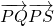 =
=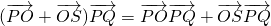
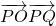 =
= ,(12分)
,(12分)
当OS∥PQ时,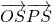 取得最大值,即
取得最大值,即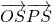 ≤
≤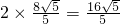
∴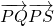 的最大值是
的最大值是 .(16分)
.(16分)
分析:(1)求弦PQ的长即先求出圆心到PQ的距离,然后根据勾股定理即可求解
(2)根据点S将上半圆分成1:2两部分圆弧时,求出点S的坐标,即可求出直线PS的方程
(3)根据向量加法知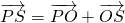 ,将
,将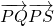 转化为
转化为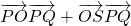 即可
即可
点评:本题考查了向量在几何中的应用,直线与圆的位置关系,向量的数量积与不等式的知识,属于基础题.
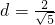
∴弦PQ=
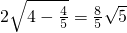 (4分)
(4分)(2)由题意得:
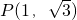 或
或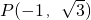 ,(6分)
,(6分)直线PS的方程为
 或
或 (8分)
(8分)(3)∵
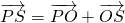
∴
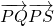 =
=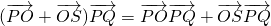
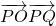 =
= ,(12分)
,(12分)当OS∥PQ时,
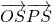 取得最大值,即
取得最大值,即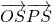 ≤
≤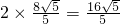
∴
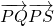 的最大值是
的最大值是 .(16分)
.(16分)分析:(1)求弦PQ的长即先求出圆心到PQ的距离,然后根据勾股定理即可求解
(2)根据点S将上半圆分成1:2两部分圆弧时,求出点S的坐标,即可求出直线PS的方程
(3)根据向量加法知
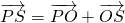 ,将
,将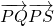 转化为
转化为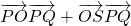 即可
即可点评:本题考查了向量在几何中的应用,直线与圆的位置关系,向量的数量积与不等式的知识,属于基础题.

练习册系列答案
相关题目
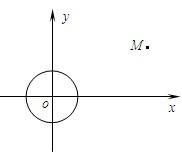 已知⊙O:x2+y2=1和点M(4,2).
已知⊙O:x2+y2=1和点M(4,2). 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.