题目内容
（2009•台州二模）若方程lnx+3x-6=0的解为x0，则关于x不等式x≥x0的最小整数解是（ ）
分析：由条件：“方程lnx+3x-6=0的解为x0”得：方程lnx=6-3x．此方程的根是两个函数y=6-3x，y=lnx图象交点的横坐标，分别画出它们的图象，由图判断知x0∈（1，2），从而得解．
解答：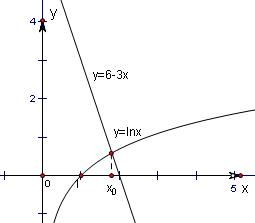
解：∵方程lnx-6+3x=0，
∴方程lnx=6-3x．分别画出两个函数y=6-3x，y=lnx的图象：
由图知两函数图象交点的横坐标即方程lnx-6+3x=0的解x0∈（1，2）．
∴不等式x≥x0的最小整数解是2．
故选B．
解：∵方程lnx-6+3x=0，∴方程lnx=6-3x．分别画出两个函数y=6-3x，y=lnx的图象：
由图知两函数图象交点的横坐标即方程lnx-6+3x=0的解x0∈（1，2）．
∴不等式x≥x0的最小整数解是2．
故选B．
点评：用函数的思想研究方程问题，关键是合理构造函数，充分利用函数的图象，体现了数形结合的思想．
练习册系列答案
相关题目
