题目内容
如图,四棱锥P-ABCD的底面为矩形,且AB=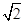 ,BC=1,E,F分别为AB,PC中点.
,BC=1,E,F分别为AB,PC中点.
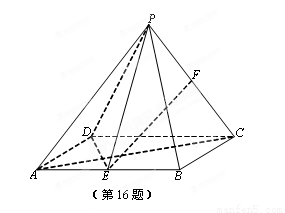
(1)求证:EF∥平面PAD;
(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.
证明:(1)方法一:取线段PD的中点M,连结FM,AM.
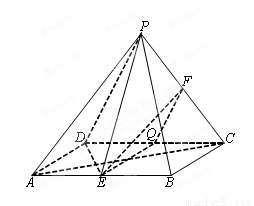
因为F为PC的中点,所以FM∥CD,且FM=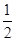 CD.
CD.
因为四边形ABCD为矩形,E为AB的中点,
所以EA∥CD,且EA=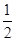 CD.
CD.
所以FM∥EA,且FM=EA.
所以四边形AEFM为平行四边形.
所以EF∥AM. ……………………… 5分
又AMÌ平面PAD,EFË平面PAD,所以EF∥平面PAD. ………7分
方法二:连结CE并延长交DA的延长线于N,连结PN.
因为四边形ABCD为矩形,所以AD∥BC,
所以∠BCE=∠ANE,∠CBE=∠NAE.
又AE=EB,所以△CEB≌△NEA.所以CE=NE.
又F为PC的中点,所以EF∥NP.………… 5分
又NPÌ平面PAD,EFË平面PAD,所以EF∥平面PAD. ……………7分
方法三:取CD的中点Q,连结FQ,EQ.
在矩形ABCD中,E为AB的中点,所以AE=DQ,且AE∥DQ.
所以四边形AEQD为平行四边形,所以EQ∥AD.
又ADÌ平面PAD,EQË平面PAD,所以EQ∥平面PAD. ………………2分
因为Q,F分别为CD,CP的中点,所以FQ∥PD.
又PDÌ平面PAD,FQË平面PAD,所以FQ∥平面PAD.
又FQ,EQÌ平面EQF,FQ∩EQ=Q,所以平面EQF∥平面PAD.…………… 5分
因为EFÌ平面EQF,所以EF∥平面PAD. ……………………………… 7分
(2)设AC,DE相交于G.
在矩形ABCD中,因为AB=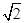 BC,E为AB的中点.所以
BC,E为AB的中点.所以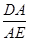 =
=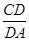 =
=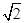 .
.
又∠DAE=∠CDA,所以△DAE∽△CDA,所以∠ADE=∠DCA.
又∠ADE+∠CDE=∠ADC=90°,所以∠DCA+∠CDE=90°.
由△DGC的内角和为180°,得∠DGC=90°.即DE⊥AC. ……………………… 10分
因为平面PAC⊥平面ABCD 因为DEÌ平面ABCD,所以DE⊥平面PAC,
又DEÌ平面PDE,所以平面PAC⊥平面PDE. ………………………… 14分
【解析】略

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB. 如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E.
如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E. 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.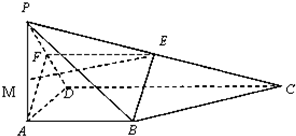 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=