题目内容
如图，四棱锥P-ABCD底面是正方形，且四个顶点A，B，C，D在球O的同一个大圆（球面被过球心的平面截得的圆叫做大圆）上，点P在球面上，且PO⊥面AC，且已知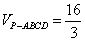
。
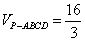
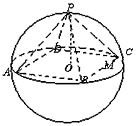
（1）求球O的体积；
（2）设M为BC中点，求异面直线AM与PC所成角的余弦值。
（2）设M为BC中点，求异面直线AM与PC所成角的余弦值。
解：（1）设球O的半径为R，则PO=OB=OC=R，
所以BC=PC=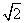
R，
∴
，
，
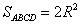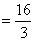所以R=2，
所以球O的体积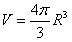
。
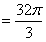（2）取PB的中点N，连结MN，AN，则MN∥PC，
所以∠AMN 为异面直线AM与PC所成的角。
由已知
，
，
，
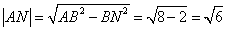所以
。
所以BC=PC=
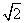R，∴
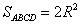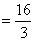，，所以R=2
所以球O的体积
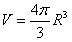
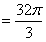。 （2）取PB的中点N，连结MN，AN，则MN∥PC，
由已知
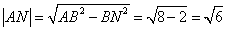，，，所以
。
练习册系列答案
阶梯计算系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=