题目内容
如图,已知椭圆C的中心在原点,焦点在x轴上,离心率为![]() ,且过点
,且过点![]() ,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
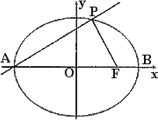
(1)求椭圆C的方程;
(2)求点P的坐标;
(3)设M是直角三角PAF的外接圆圆心,求椭圆C上的点到点M的距离d的最小值.
答案:
解析:
解析:
解:(1).![]() (4分)
(4分)
(2)由已知可得点A(-6,0),F(4,0)
设点P的坐标是![]() ,由已知得
,由已知得
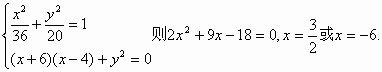
由于![]() (9分)
(9分)
(3)点M的坐标是(-1,0),椭圆上的点![]() 到点M的距离d有
到点M的距离d有![]()
由于![]() (14分)
(14分)

练习册系列答案
相关题目
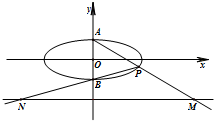 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
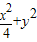 =1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;
=1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;
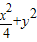 =1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;
=1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;