题目内容
已知对任意x∈R,不等式
>(
)2X2-mx+m+4恒成立,求实数m的取值范围.
| 1 |
| 2X2+X |
| 1 |
| 2 |
分析:化简不等式,利用指数函数的单调性,转化不等式为二次不等式,通过判别式解决恒成立问题,求出m的范围.
解答:解:原不等式为(
)x2+x>(
)2x2-mx+m+4,由函数y=(
)x是减函数…(4分)
得x2+x<2x2-mx+m+4恒成立,…(6分)
即x2-(m+1)x+m+4>0恒成立,…(8分)
∴△=(m+1)2-4(m+4)<0…(10分)
∴-3<m<5…(12分)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
得x2+x<2x2-mx+m+4恒成立,…(6分)
即x2-(m+1)x+m+4>0恒成立,…(8分)
∴△=(m+1)2-4(m+4)<0…(10分)
∴-3<m<5…(12分)
点评:本题考查指数函数的性质,恒成立条件的应用,二次不等式的解法,考查计算能力.

练习册系列答案
相关题目
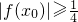 成立.
成立.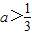
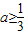
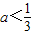
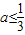
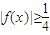 成立.
成立.