Question

已知集合P={x|1≤x≤8,x∈Z}，直线y=2x+1与双曲线mx²-ny²=1有且只有一个公共点，其中m,n∈P，则满足上述条件的双曲线共有______________个

A.1                     B.2                    C.3                   D.4

Answer 1

答案：D  P={1，2，3，4，5，6，7，8}.

①∵直线y=2x+1的斜率k=2且过点(0，1).故当双曲线mx²-ny²=1的渐近线的斜率为2时，直线与双曲线只有一个交点,即=2,∴=4，此时m=4，n=1或m=8，n=2.

②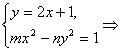(m-4n)x²-4nx-(n+1)=0，令Δ=16n²+4(n+1)(m-4n)=0,得m=,故n=1,m=2或n=3,m=4.

∴共有4个.