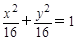题目内容
已知点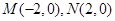 ,动点
,动点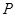 满足条件
满足条件 .记动点
.记动点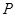 的轨迹为
的轨迹为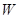 .
.
(Ⅰ)求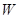 的方程;
的方程;
(Ⅱ)若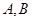 是
是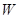 上的不同两点,
上的不同两点,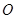 是坐标原点,求
是坐标原点,求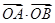 的最小值.
的最小值.
【答案】
(1)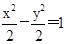 (x>0)(2)
(x>0)(2)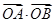 的最小值为2
的最小值为2
【解析】本试题主要是根据定义求解双曲线的方程,以及直线与双曲线的位置关系的综合运用。
(1)根据题意,点P的轨迹是以M,N为焦点的双曲线的右支,所求方程为: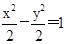 (x>0)
(x>0)
(1) (2)当直线AB的斜率不存在时,设直线AB的方程为x=x0,此时A(x0,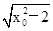 ),
),
B(x0,-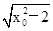 ),
),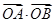 =2
=2
当直线AB的斜率存在时,设直线AB的方程为y=kx+b,代入双曲线方程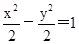 中,得:(1-k2)x2-2kbx-b2-2=0,结合韦达定理和向量的数量积公式得到求解
中,得:(1-k2)x2-2kbx-b2-2=0,结合韦达定理和向量的数量积公式得到求解

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
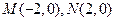 ,动点
,动点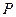 满足条件
满足条件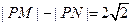 .记动点
.记动点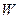 .
.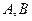 是
是 是坐标原点,求
是坐标原点,求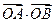 的最小值.
的最小值.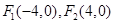 ,动点
,动点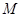 满足条件:
满足条件: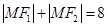 ,则点
,则点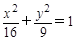 B.
B.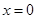 C.
C.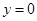 (
(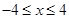 ) D.
) D.