题目内容
若a,b,c为不全相等的正数,求证:lg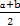 +lg
+lg +lg
+lg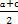 >lga+lgb+lgc.
>lga+lgb+lgc.
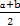 +lg
+lg +lg
+lg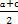 >lga+lgb+lgc.
>lga+lgb+lgc.见解析
证明:由a,b,c为正数,得lg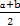 ≥lg
≥lg ;lg
;lg ≥lg
≥lg ;lg
;lg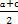 ≥lg
≥lg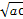 .
.
而a,b,c不全相等,
所以lg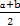 +lg
+lg +lg
+lg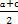 >lg
>lg +lg
+lg +lg
+lg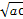 ="lg" (abc)=lga+lgb+lgc.
="lg" (abc)=lga+lgb+lgc.
即lg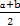 +lg
+lg +lg
+lg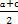 >lga+lgb+lgc.
>lga+lgb+lgc.
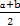 ≥lg
≥lg ;lg
;lg ≥lg
≥lg ;lg
;lg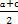 ≥lg
≥lg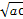 .
.而a,b,c不全相等,
所以lg
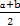 +lg
+lg +lg
+lg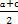 >lg
>lg +lg
+lg +lg
+lg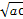 ="lg" (abc)=lga+lgb+lgc.
="lg" (abc)=lga+lgb+lgc.即lg
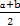 +lg
+lg +lg
+lg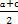 >lga+lgb+lgc.
>lga+lgb+lgc.
练习册系列答案
相关题目
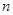 个图形中有
个图形中有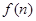 .
.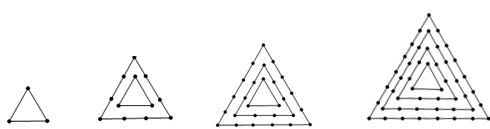
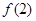 ,
,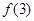 ,
,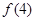 ,
, ;
;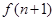 的关系,并求出
的关系,并求出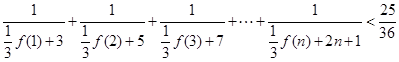 (
(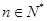 ).
).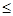
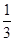 ;
;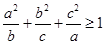
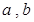 为实数,证明:
为实数,证明: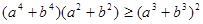 .
. 均为实数,且
均为实数,且 ,求证:
,求证: 。
。