题目内容
某市为响应国家节能减排,建设资源节约型社会的号召,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告:
(一)80部手机,一年就会增加一吨二氧化碳的排放…
(二)人们在享受汽车带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气…
活动组织者为了解市民对这两则广告的宣传效果,随机对10~60岁的人群抽查了n人,统计结果如下图表:
(1)分别写出n,a,c,d的值;
(2)若以表中的频率近似看作各年龄组正确回答广告内容的概率,规定正确回答广告一的内容得20元,正确回答广告二的内容得30元.组织者随机请一个家庭中的两名成员(大人45岁,孩子17岁)回答这两则广告的内容,求该家庭获得奖金的期望(各人之间,两则广告之间,对能否正确回答均无影响).
(一)80部手机,一年就会增加一吨二氧化碳的排放…
(二)人们在享受汽车带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气…
活动组织者为了解市民对这两则广告的宣传效果,随机对10~60岁的人群抽查了n人,统计结果如下图表:
| 广告一 | 广告二 | |||
| 回答正 确人数 |
占本组 人数频率 |
回答正 确人数 |
占本组 人数频率 | |
| [10,20) | 90 | 0.5 | 45 | a |
| [20,30) | 225 | 0.75 | k | 0.8 |
| [30,40) | b | 0.9 | 252 | 0.6 |
| [40,50) | 160 | c | 120 | d |
| [50,60] | 10 | e | f | g |
(2)若以表中的频率近似看作各年龄组正确回答广告内容的概率,规定正确回答广告一的内容得20元,正确回答广告二的内容得30元.组织者随机请一个家庭中的两名成员(大人45岁,孩子17岁)回答这两则广告的内容,求该家庭获得奖金的期望(各人之间,两则广告之间,对能否正确回答均无影响).
分析:(1)由题设知:n=1200,a=
,c=
,d=
.
(2)依题意,孩子正确回答广告一、广告二的内容的概率分别为P1=
,P2=
,大人正确回答广告一、广告二的内容的概率分别为P3=
,P4=
,设随机变量ξ表示家庭获得的奖金数,则ξ的可能取值为:0,20,30,40,50,60,70,80,100.由此能求出ξ的分布列和Eξ.
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
(2)依题意,孩子正确回答广告一、广告二的内容的概率分别为P1=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
解答:解:(1)由题设知:n=1200,a=
,c=
,d=
.
(2)依题意,孩子正确回答广告一、广告二的内容的概率分别为P1=
,P2=
,
大人正确回答广告一、广告二的内容的概率分别为P3=
,P4=
,
设随机变量ξ表示家庭获得的奖金数,
则ξ的可能取值为:0,20,30,40,50,60,70,80,100.
P(ξ=0)=(1-
)×(1-
)×(1-
)(1-
)=
,
P(ξ=20)=
×(1-
)×(1-
)× (1-
)+(1-
)×(1-
)×
×(1-
)=
,
P(ξ=30)=(1-
)×
×(1-
)×(1-
)+(1-
)×(1-
)×(1-
)×
=
,
P(ξ=40)=
×(1-
)×
×(1-
)=
,
P(ξ=50)=
×
×(1-
)×(1-
)+
×(1-
)× (1-
)×
+(1-
)×
×
×(1-
)+(1-
)× (1-
)×
×
=
,
P(ξ=60)=(1-
)×
× (1-
)×
=
,
P(ξ=70)=
×
×
×(1-
)+
×(1-
)×
×
=
,
P(ξ=80)=
×
× (1-
)×
+(1-
)×
×
×
=
,
P(ξ=100)=
×
×
×
=
.
∴ξ的分布列为:
Eξ=0×
+20×
+30×
+40×
+50×
+60×
+70×
+80×
+100×
=
(元).
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
(2)依题意,孩子正确回答广告一、广告二的内容的概率分别为P1=
| 1 |
| 2 |
| 1 |
| 4 |
大人正确回答广告一、广告二的内容的概率分别为P3=
| 2 |
| 3 |
| 1 |
| 2 |
设随机变量ξ表示家庭获得的奖金数,
则ξ的可能取值为:0,20,30,40,50,60,70,80,100.
P(ξ=0)=(1-
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 16 |
P(ξ=20)=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 16 |
P(ξ=30)=(1-
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 12 |
P(ξ=40)=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 8 |
P(ξ=50)=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
+(1-
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
P(ξ=60)=(1-
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 48 |
P(ξ=70)=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
P(ξ=80)=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 16 |
P(ξ=100)=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 24 |
∴ξ的分布列为:
| ξ | 0 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 100 | ||||||||||||||||||
| P |
|
|
|
|
|
|
|
|
|
| 1 |
| 16 |
| 3 |
| 16 |
| 1 |
| 12 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 48 |
| 1 |
| 6 |
| 1 |
| 16 |
| 1 |
| 24 |
| 275 |
| 6 |
点评:本题考查离散型分布列的数学期望和方差,是历年高考的必考题型.解题时要认真审题,仔细解答,注意概率知识的灵活运用.

练习册系列答案
相关题目
某市为响应国家节能减排,建设资源节约型社会的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告:
(一)80部手机,一年就会增加一吨二氧化碳的排放。……
(二)人们在享受汽车带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气。……
|
(I)分别写出n,a,c,d的值;
(II)若以表中的频率近似看作各年龄组正确回答广告内容的概率,规定正确回答广告一的内容得20元,广告二的内容得30元。组织者随机请一家庭的两成员(大人45岁,孩子17岁)回答两广告内容,求该家庭获得奖金的期望(各人之间,两广告之间,对能否正确回答,均无影响。)

 带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于
带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于 年起取消
年起取消 排放量超过
排放量超过 的
的 型新车挂牌.检测单位对目前该市保有量最大的甲类
型新车挂牌.检测单位对目前该市保有量最大的甲类 辆进行了
辆进行了 记录如下(单位:
记录如下(单位: ).
).
 ,求
,求 的值及样本标准差;
的值及样本标准差;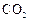 排放量的概率是多少?
排放量的概率是多少? 年起取消
年起取消 排放量超过
排放量超过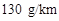 的
的 型新车挂牌.检测单位对目前该市保有量最大的甲类
型新车挂牌.检测单位对目前该市保有量最大的甲类 辆进行了
辆进行了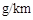 ).
).
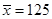 ,求
,求 的值及样本标准差;
的值及样本标准差; 排放量的概率是多少?
排放量的概率是多少?