题目内容
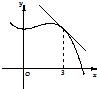4、如图，y=f（x）的图象在点P处的切线方程为y=-x+6，f′（x）是f（x）的导函数则f（3）+f'（3）=（ ）分析：根据图象把切线方程变形即可得到切线的斜率k的值得到f′（3）的值，也得到切点P的坐标得到f（3）的值，求出之和即可．
解答：解：由y=f（x）的图象在点P处的切线方程为y=-x+6，变形得：y-3=-（x-3），
根据图象可得：切线斜率k=-1=f′（3）；切点坐标P（3，3），所以f（3）=3．
则f（3）+f'（3）=3+（-1）=2
故选C
根据图象可得：切线斜率k=-1=f′（3）；切点坐标P（3，3），所以f（3）=3．
则f（3）+f'（3）=3+（-1）=2
故选C
点评：考查学生会利用导数研究曲线上某点的切线方程，理解函数值的意义．会利用数形结合的数学思想解决实际问题．
练习册系列答案
相关题目
16、如图是y=f（x）的导数的图象，则正确的判断是
如图是y=f'（x）的图象，则y=f（x）的大致图象是（ ）
如图函数y=f（x）的图象在点P处的切线的方程为y=-2x+9，则f（4）+f'（4）的值是（ ）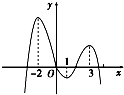
如图为y=f（x）的图象，则它的单调递减区间是